BUILDING BRIDGES
An architect that constructs bridges has to think carefully about a lot of thinks before sketching a bridge. One of them is the geometry of bridges. Can you help him creating a model of an arcuate bridge? How can we create an arc? What and how does it change in an arc? Can I know in advance its length, its breadth or its curvature? With the microworld ‘bridges’ you can start with a program creating arcs. Can you amend it so as to create a model of bridges for the architect? He will really appreciate that! This activity is one of the most favourites in our schools. It has been applied at the end of primary school and at the first level of high school. Students experiment with the notion of geometric arc and find out gradually its basic properties: the notion of curvature, length and breadth of the arc,
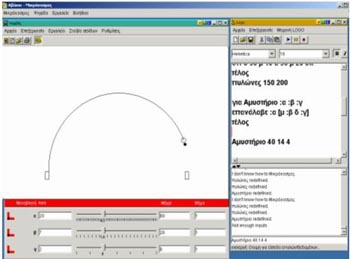the notion of the polygonal approach of curve, the notion of arc and string and many other notions needed for the use and understanding of the notions mentioned before. In their experimentation students make use of symbolic and graphical representations. Students create parametric procedures and manipulate tools that change dynamically the graphical representations as the value of the parameter changes in an apparent continuous way. Thus they create a bridges' "machine" that can change the number and the constitutive elements of an arcuate bridge. Finally, students discuss their conclusions and create many bridges that can be enriched by free sketching.
download
-------------------------------------------------------------------------------------------------
THE TREASURE HUNT GAME
The treasure hunt game is exciting and has been played by most of us. With the software ‘map constructor’ not can youcreate that game but you can create it at many versions as well! You can define your own rules, draw a map choosing your own area and insert whatever object you want. You can contrive your own riddles and your own treasure! The activity 'treasure hunt' aims at the development of small but multi-dimensional software and was applied at the second level of high-school. In the beginning students play the role of a cartographer. They draw the contour of the buildings of an area using parametric procedures that drive the 'turtle'–grapher in the screen. They put them in a scale of their own choice paying
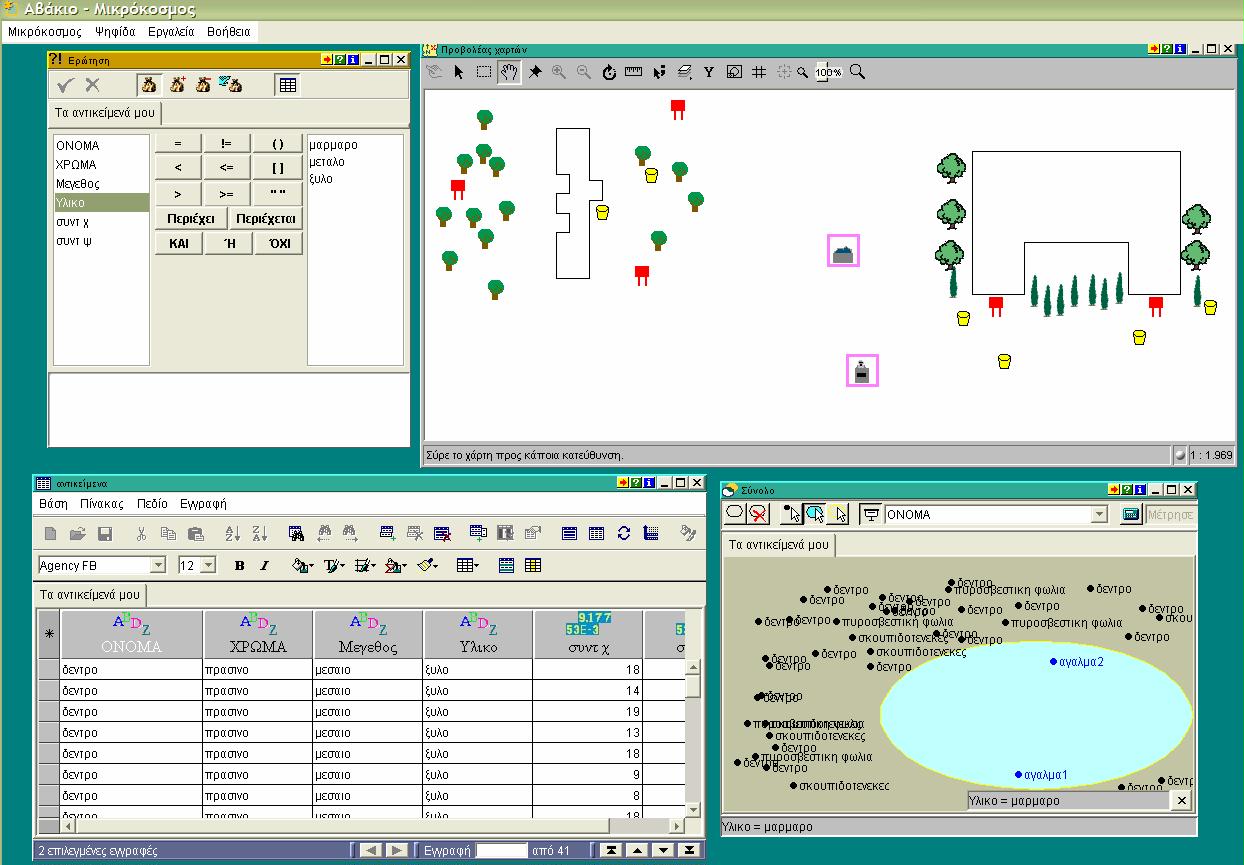also attention to keep the orientation and the distances also in scale, experimenting and changing the values of parameters using tools of dynamic manipulation. Thus they use the notion of scale, of orientation, of ratio and of systems of reference. Then they choose the objects that they want to chart, they insert the relative objects in the map and they connect the images with information about those objects. Finally they pose their own riddles –that they presuppose the processing of the information through the software for the detection of objects – and they play the game of treasure hunt. It is an interdisciplinary activity centre on spatial thinking, orientation and symbolic representation of spatial objects and relations.
download