 |
SLIDERS
|
Each one of the sliders 1,2 and 3 depends in a certain way on the first slider, this one without a number. Can you find the dependence relation sliding the first slider and observing what happens with each one of the others? How is the observable velocity of each one connected to this relation? Invent your own dependence relations and replace the one above. Ask your classmates to find them out.
This activity includes the notion of co-variation and of function graphically represented in an unconventional way. This representation is not static. It is apparent only when the student slides dynamically the pinpoint of the independent variable and observes the differences in motion between the dependent ones. This activity could be
|
 |
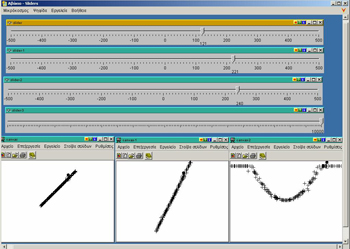 |
| appropriate for high school students, depending on the complexity of the initial function. Students can change function’s relations altering a simple symbolic procedure. They can experiment with any function as the alterations of limits of the domain of definition of sliders are easy. They can play the game ‘guess my function’. They can also represent the notion of functions’ composition setting each slider in dependence of the immediately previous one. This alternative representation and its comparison to the orthonormal system of axis let students go into the understanding of notions of systematic mathematical relations, of co-variation and of other notions related to function. |
download


 |
-------------------------------------------------------------------------------------------------
|
THE JUGGLER
|
Come and play with the juggler! We need at least two players. What you need to do? Just don't let the ball fall down from the juggler’s hands. And how does the ball move? How does it reflect on the juggler's hands? What changes can you apply to the rules of the game so that it becomes easier or harder for your co-player?
Ôhe juggler is mainly addressed to students aged 12-14 (2nd year of greek Gymnasium – secondary education) and beyond. The activity has two levels: on a primary level, you play the game against the computer, while on a second one –which is definitely more interesting- you change the game rules and give it to your co-player to see what he or she can do! What can be changed? The number of balls, or even, the
|
 |
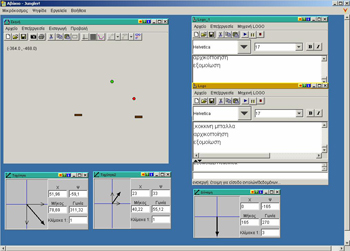 |
| number of hands, the rules of the ball motion, the rules of the ball percussion against the hand and the gravity rules for each ball. By changing the rules, you deeply think about how govern the motions and the conduct of the bodies, you experiment, and you can even see what could have happened if Newton wasn’t so right after all! You can design "tricks" for your co-player and ask him or her to guess what is it that you’ve changed. |
download



|
|
 |