An Online Setting for Exploring, Constructing, Sharing and Learning Mathematical Ideas

Marco A. Olivera, marco.pumas@gmail.com

Dept. of Mathematics Education, Center for Research and Advanced Studies (Cinvestav)

Ana Isabel Sacristán, asacrist@cinvestav.mx

Dept. of Mathematics Education, Center for Research and Advanced Studies (Cinvestav)

Abstract

We present here an on-going research project on mathematical learning through a process of building math models in a context of rich experimentation and virtual collaboration in an online environment. Our design ideas aim to 1) harness the potential of technological tools for exploration, discovery and learning; 2) use the Internet and social networks as a means of virtual communication and collaboration. Although online distance education is becoming more prevalent, this type of virtual collaboration for learning hasn’t yet been exploited much in our country (Mexico). We present the fundamental design of our setting, research objectives and sample activities.

Keywords

Technology-enhanced learning, mathematics, collaboration, constructionism, distance education

 Introduction and research objectives

For the past couple of years, we have been working on building an Internet-mediated laboratory for experimentation and virtual collaboration, in which students can explore mathematical problems. Sciences such as physics, chemistry, etc. depend on research carried out in laboratories; but in mathematics, research is done through an idealized world where the tool for discovery is intuition (Klarreich, 2004). Thus our objective has been in developing and researching a virtual setting (an “online lab”) where technology is used in a two-fold way: as a tool for local experimentation; and as a vehicle for communication and collaboration.

We present here parts on-going study that aims to investigate how students can explore mathematical ideas through experimentation and virtual collaboration (via a social network), which may lead to insights and discoveries that can be more difficult through traditional media. The main purpose is to encourage students to make discoveries and build knowledge, following the constructionist paradigm (Papert & Harel, 1991), in a technological environment that is conceived as a research laboratory where, through computer programming and construction (which can involve processes such as trial and error, debugging and feedback) learning can be enhanced (see also Hitt, 2003; or Sacristán et al., 2010). Online blogs and social networks are used so that participants can collaborate on a task or set of problems related to a particular topic, sharing their ideas, knowledge and expertise.

It is remarkable how thirty years ago, Papert (1980) had already proposed that computer microworlds could be used in this way and for constructionism. Nowadays, the affordances of digital technologies are more powerful and readily available, in particular allowing virtual collaboration and communication. In spite of the growing tendency in the use of virtual settings in education, “constructionist online collaboration” is still rare; thus, we believe that the potential of virtual collaboration, as such, can be exploited much more in education and may be attractive to students in all levels who are already immersed in the dynamics of social networks. For this, we have designed a web-based educational platform that has, as basic elements, tools for collaboration, communication (including a discussion forum and blogs) – see Figures 1 and 2 –and a repository of various types of documents (e.g. tasks, programming activities, images, videos sharing, the activity software files, etc.).

Figure 1: Social network tools of the virtual setting	Figure 2: Portal to one of the explorations on the platform including to its forums and blogs

As already stated above, in our project, we use technology as a tool for exploring and constructing mathematical ideas; and as a tool for communication and collaboration. The key objectives of our study are thus twofold: 1. To encourage experimentation, collaboration and reflection of mathematical problems among virtual community members. 2. To analyze how these processes can promote learning in the participants. This analysis includes looking at the role of the computational and ICT tools in the development, exploration and learning of the mathematical ideas studied in the virtual environment; what thinking processes and attitudes are developed; but also what difficulties are encountered in the execution of the virtual collaborative activities.

Background and theoretical framework: Constructing, sharing and learning

As stated above, our main theoretical principle is the constructionist paradigm. Thus, we define our virtual exploratory environment as a place where one can create, execute and disseminate mathematical experiments across a computing infrastructure consisting of a set of programmable objects. Jeschke, Richter & Seiler (2005) define the concept of a virtual laboratory in mathematics and social sciences as a set of interactive tools that achieve learning through exploration. Some authors, such as Schmid et al. (2001), have designed virtual labs where they can perform simulations, interactive animations, and experiments. Other studies, such as those of Hoffman et. al (1994) and Sánchez et. al. (2002), combine laboratory experiments with computer simulations and experimentations that involve the manipulation of various physical tools controlled remotely via a web platform.

In our study, the context in which the mathematical activities take place, as well as the social forms of interaction, are as important as the tasks themselves (Hoyles & Noss, 1987). Thus our activities take place in a type of social network, where participants can share a concern or set of problems on a topic and deepen their knowledge and expertise through a social structure based on collaboration – akin to what can happen in Wenger’s (1998) communities of practice. In other words, the key aspect is a collaborative learning strategy: a carefully designed system to organize and lead the interactions between team members (Johnson & Johnson, 1997). Collaborative learning is developed through a gradual process in which members can feel mutually committed to the learning of others, creating a positive interdependence not involving competition (Lucero et. al, 2003; Crook, 1998; Johnson & Johnson, 1997). In our project, most of this collaboration takes place virtually.

It is worth noting that a main inspiration and background study for our research was that of the WebLabs project, which was a European research project in mathematics education involving schools and research institutions in six countries. In that project, a community of students, teachers and researchers worked collaboratively exploring mathematical ideas and scientific phenomena through computational and virtual infrastructures (see Matos et. al. 2003; Sendova et al., 2004; Kahn, 2004; Mousolides et. al, 2005; Simpson, Hoyles and Noss, 2005; Mor et al., 2006). The aim of Weblabs was to investigate new representational infrastructures for constructing, sharing and learning mathematical and scientific ideas. Since the design and conception of the WebLabs project, included many of the same theoretical and methodological ideas that we support (such as a constructionist use of technology, and collaboration in virtual communities), we have used it as a basis for our research.

In terms of the mathematical explorations and tasks, many these are conceived to promote learning through the building of models. What is meant by modelling? This can be understood in several ways. First, it can be understood as the construction of a mathematical model, thus bridging real world phenomena with the mathematical world:

Mathematical modeling is a process of representing real world problems in mathematical terms in an attempt to find solutions to the problems. A mathematical model can be considered as a simplification or abstraction of a (complex) real world problem or situation into a mathematical form, thereby converting the real world problem into a mathematical problem. (Ang, 2001, p. 64)

But modelling can be used, not only to “find solutions” but, as Epstein (2008) emphasizes, to explain phenomena. Therefore models and their representations can be of different levels of complexity and/or accuracy (i.e. more mathematically-dependent or less). Lesh and Doerr (2003, p.10) explain that: “Models are conceptual systems … that are used to construct, describe, or explain the behavior” of a system. Thus, modelling is a powerful tool that can enhance the principles of scientific thinking (Aris, 1994). That is, creating one’s own models can be a powerful learning experience that can help to better understand the world around us. Digital technologies have provided a new medium for building, analyzing, and describing models; they make it easier to build and explore one’s own models and learn new scientific ideas in the process (Colella, Klopfer, & Resnick, 2001). One example of the possible constructionist nature of modelling real world problems, and of its potentials for learning, is described by Noss and Hoyles (1996) in relation to computer-based tasks related to modelling the mathematics of banking:

Throughout the work, our students constructed and reconstructed the resources we provided, and explored and expressed regularities and structures they encountered. We gave them the simple programs as building blocks, but they edited them, switched variables and parameters, and recombined these blocks to model financial situations, some of which were strange to our eyes […] the mathematical and banking ideas came to be woven together to produce a powerful synergy, making both the mathematics and the structures of banking practices more visible. The power of the computational modelling approach was that it facilitated this interconnection: students could interlace their banking knowledge with the mathematical ideas we intended to teach and in the process take control of the direction of their investigations. (Noss & Hoyles, 1996, p. 29)

Lesh and Doerr (2000) claim that some of the key components involved in models and modelling are symbolizing, communicating and mathematizing. We want to exploit these in our project so that the tasks in our online lab provide our students with the opportunity to engage in activities as mathematicians (Papert, 1972): by symbolizing ideas in the problem, sharing and discussing their findings with peers, and refining their proposed model.

The mathematical activities

We have currently been designing exploratory activities for high-school and university students (although in later phases of the project we would like to also work with younger students). In the design of the activities, we have been concerned on how to design thematic lines or mathematics explorations to enhance motivation and continuous reflection through the virtual environment. We have thus been concerned with two things: the mathematical ideas to be studied; and how to carry out the explorations of those mathematical ideas. Therefore, we have been designing computer-based exploratory hypothetical learning trajectories (Simon, 1995) of several mathematical topics (e.g. see Figure 3); the topics we have chosen are such so that they have the potential to generate several problems for analysis, and may promote discussion among members of a virtual community allowing in turn for the emergence of new issues to be analyzed. Some of the explorations topics we have been working on, are: uniform rectilinear motion with cars; cryptography (decoding hidden messages using frequency statistics); and the population growth of spotted owls. For the explorations, we draw from a variety of technological tools (depending on the activity) to explore ideas and build models, including Modellus (see below), Logo, NetLogo, Excel and e-Slate. We present below some sample activities from our study.

The Population of Spotted Owls[1]

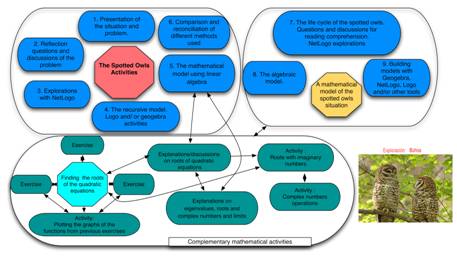
Figure 3: Schematic of the owls’ population activities and learning trajectories

The details of this exploration are beyond the scope of this paper, but we include some of them here because this is a real-life problem that can be used to introduce students to many mathematical topics, but is, particularly, an example of a use of complex numbers. The mathematical model[2] centres on a system of recursive equations involving populations of rats and owls, where O_k is the owl´s population at time k; R_k is the rat´s population at time k; and p is an unknown positive number:

 

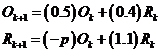
Time (months)	Owl´s Population (O)	Rat´s Population (R)	Rate (Rat´s population /Owl´s Population)
1
2
3

Table 1: Populations of owls and rats through time

One of the first tasks is to fill a table (similar to the one shown in Table 1) that can help students – using the NetLogo (http://ccl.northwestern.edu/netlogo/) multi-agent programmable modelling environment –  modify, as necessary, a Population Dynamics program to do a simplified model of this Owls and Rats situation.  In order to properly solve the set of equations, linear algebra is required (leading to a solution involving complex numbers). So this is an opportunity to introduce themes of linear algebra to students, through the eigenvectors and eigenvalues of the matrix:

 Or, at another level, through the following matrix equation, where J_k is the female population of very young owls in the k time; S_k is the is the female population of middle age owls in the k time; and a_k is the female population of old age owls in the k time:

The Free Fall explorations

The Free fall activity (which is a much-exploited activity in mathematics and science education) is intended for exploration of the movement of an object being dropped down. The purpose of the activity is for students to construct a mathematical model to express the relationship between time and height, such as the equation  h= g .(t2) / 2, 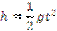 where h is the height, t is the time-interval, and g is the gravity constant. The explorations use Modellus, a free software from Portugal (http://modellus.fct.unl.pt/), for which we provide a link on our platform. Students have to record a video of the free fall of a ball (or other object), using a video camera, upload it unto the Modellus system, and analyze the mechanics of the experimental data, first locally, on their own computers, and then through virtual collaboration (see below). The Modellus software allows for analysis of the distance from the origin and the floor, at different time intervals (see Figure 4), so that the speed in each interval can be inferred, and eventually they might discover that there is a constant (the gravity constant).

Figure 4: Analysis, using Modellus, of a person dropping a ball.

Figure 5: Blog of the “Free fall” activity.

On the platform we provide a worksheet with reflection questions regarding the activity, as well as suggestions of different working tables; using the questions and tools on the worksheets as guidelines, students then write down, on a blog (Figure 5), their inferences about the phenomena derived from their explorations using the software; they can add their videos, files and screen captures. They can then participate in online virtual collaborative discussions, sharing ideas and analyzing each other’s data and conclusions, in order to refine their individual models and construct a collaborative model of the phenomenon  

In summary, the purpose is for students to collaboratively build a mathematical model of the free-fall phenomenon, through a hypothetical learning trajectory that involves processes of: getting data, discussing their findings through the blog, the forum, when possible video-conferences, and then test their model using the Modellus software; this is a cyclical process until a mutual agreement is reached on a mathematical model that best describes the phenomena, and finding the gravity constant. This activity is followed by a second activity to discover the gravity constant on the Moon, by analyzing videos of a man jumping on the Moon.

The Moving Cars explorations

The Moving Cars activity is intended for students to explore linear motion with constant speed, and model it through a mathematical process of experimentation. The phenomenon of uniform rectilinear movement encompasses a wealth of mathematical ideas to be explored and experimented by students, and yet is a real phenomenon that can be modelled using basic equations. For this activity we also use the Modellus environment.

The tasks in this activity are of two kinds:

§  Initial exploration tasks, proposed by the teacher.

§  Open exploration tasks proposed by the students.

The first group of tasks is intended to provide students with the intuition of "uniform rectilinear motion with constant velocity". For this, we start from different situations: A first situation is given by providing a Modellus model (see Figure 6), with two moving vehicles that begin their journey at the same time with different speeds (for example, car A has a speed of 5 km/hr, while car B has a speed of 7 km/hr).

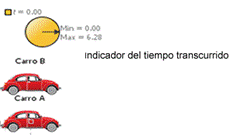
Figure 6: Exploration of the movement of two cars with the Modellus software

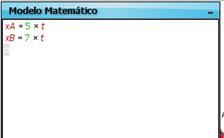
Figure 7: Defining the mathematical equations of the distance covered by each car

Figure 8: Graph and table of the distance covered in function of the time

Students can define the mathematical equations of the distance covered by each car, as shown in Figure 7. In Modellus they can also build a table of distance covered by each car in function of the time (see Figure 8). Some of the explorations that are suggested refer to the question: After how long will the vehicles be separated by an x distance (for example, by 80, 90, or 150 miles)? To answer this, students must manipulate the mathematical objects, define new mathematical equations by creating another variable which measures the distance between objects, and, at a higher level, solving an equation. During the explorations, they can use exploration tools, such as the one to measure distances (see Figure 9), or the one (see Figure 10) for defining distances (a function) by parts (see Figure 11).

Figure 9: Modellus tool to measure distances	Figure 10: Modellus tool to define a function by parts	Figure 11: Distance defined by parts, considering time intervals

The second group of tasks (those proposed by students for other students) is intended for students to explore their own ideas and socialize with their peers, thus promoting collaborative work. Some ideas for this, include students proposing a graph to other students (over the virtual platform), and asking the other students to find/build a model or mathematical equations that fits the graph; or viceversa: proposing the mathematical equations of the model and then asking their peers to describe a situation that fits these.

Methodological aspects and preliminary results

Currently we are working with a learning community that consists of 60 adult continuing education students enrolled in a distance (online) open university system (www.abiertayadistancia.sep.gob.mx – launched two years ago by the Mexican Ministry of Education), studying towards a degree in Mathematics. These students are finishing their second year of studies, and constitute a very mixed community of students of all ages and backgrounds and are located in different parts of the country. These are subjects who are, to some degree, familiar with self-study and with the use of different tools used in distance education, such as a learning platforms and forums, etc, since the distance university system is based on Moodle. However, for our study we chose not to use Moodle since we found it limited in terms of social networking capabilities and for virtual collaboration; we thus have our own platform (http://imat.cinvestav.mx).

One of the approaches for the data analysis is based on the documentary approach proposed by Gueudet and Trouche (2009) who consider that the analysis of documents (which in our case are all of the participants’ contributions on the virtual platform: e.g. comments on forums; messages – which include written interviews from our part; blogs; development of computational objects or codes; approaches to the problems; etc.) should consider the following components: the material component (i.e. the set of resources used in the educational activity), the mathematical component (the concepts and activities involved the study) and the dialectical component (which includes the organization and planning of the activity).

So far, 27 of the 60 students (with an interesting age range from 20 to 70 years old) have volunteered to take part in our study, with more signing up every day. We have divided these students to participate in the different activities. A first group, consisting of 6 students, have been working on the Moving Cars explorations. Below we give some initial findings from this group.

First, there were initial difficulties in the proposed collaborative and exploratory model of working, because this is very unusual in the Mexican educational system. Participants are thus used to simply following detailed instructions from a teacher, solving some activities individually and expecting a grade. To collaborate virtually, was even stranger for them. So one of the first obstacles was for them to understand this new working paradigm and that it wasn’t “solving a problem that would be graded”. However, gradually the participants have been getting used to the activities and began engaging first in discussions on what it means to build a mathematical model. Through these discussions they identified (as a virtual group) that there have to be elements such as variables and equations that describe a mathematical model; and, individually, they began building their models in Modellus, such as the case of Judy who published in her individual blog on the platform, an image of her model (Figure 12).

There also had discussions on the forums in relation to the concepts of speed and velocity, as well as on the meaning and interpretation of the graphs. Thus we are beginning to see good results from the virtual activities in the sense that there is collective reflection and discussion on the meanings of the activities, concepts and elements involved. A student also proposed a model for the use of a taxi, involving distance, time and cost; this has also led to discussions among the members. Work continues and we hope to achieve further positive results and meaningful learning and constructions.

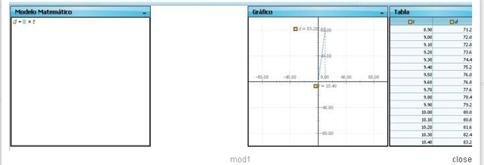
Figure 12: Judy’s first model in Modellus

References

Ang, K. C. (2001). Teaching mathematical modelling in Singapore schools. The Mathematics Educator, 6(1), 63-75.

Aris, R. (1994). Mathematical modelling techniques. NY: Dover.

Colella, V. S., Klopfer, E., & Resnick, M. (2001). Adventures in Modeling: Exploring Complex, Dynamic Systems with StarLogo. Williston, VT: Teachers College Press.

Crook, C. (1998). Ordenadores y aprendizaje colaborativo. Madrid: Morata.

Epstein, J. M. (2008). 'Why Model?'. Journal of Artificial Societies and Social Simulation 11(4)12 Retrieved from http://jasss.soc.surrey.ac.uk/11/4/12.html

Gueudet, G., & Trouche, L. (2009). Towards new documentation systems for mathematics teachers?, Educational Studies in Mathematics, 71 (3), 199-218.

Hitt, F. (2003). Una Reflexión sobre la construcción de conceptos catemáticos en ambientes de programación con tecnología. Boletín de la Asociación Matemática Venezolana, 10(2), 213-223.

Hoffman, C. M., Houstis, E. N., Rice, J. R., Catlin, A. C., Gaitatzes, M., & Weerawarana, S. (1994). SoftLab - A virtual laboratory for computational science, Mathematics and Computers in Simulation 36 (4-6), 479-491.

Hoyles, C., & Noss, R. (1987). Synthesizing mathematical conceptions and their formalization through the construction of a Logo-based school mathematics curriculum. International Journal of Mathematical Education in Science and Technology, 18(4), 581-595.

Jeschke, S., Richter, T. & Seiler, R. (2005). VIDEOEASEL: Architecture of virtual laboratories on mathematics and natural sciences. Proc. 3rd International Conference on Multimedia and ICTs in Education (pp. 874-878). Caceres/Badajos: FORMATEX.

Johnson, D. W., & Johnson, F. P. (1997). Joining together: group theory and group skills (6th ed.). Boston: Allyn & Bacon.

Kahn, K. (2004). Toontalk-steps towards ideal computer-based learning environments. In L. Steels and M. Tokoro (Eds), A Learning Zone of One's Own: Sharing Representations and Flow in Collaborative Learning Environments (pp. 253-270). Amsterdam: IOS Press.

Lesh, R., & Doerr, H. (2000). Symbolizing, communicating, and mathematizing: Key components of models and modeling. In P. Cobb, E. Yackel, & K. McClain (Eds.), Symbolizing and communicating in mathematics classrooms: Perspectives on discourse, tools, and instructional design (pp. 361–384). Mahwah,  NJ: Lawrence Erlbaum Associates.

Lesh, R. & Doerr, H. M. (2003). Foundations of models and modeling perspectives on mathematics teaching, learning, and problem solving. In R. Lesh & H. Doerr (Eds.), Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning, and teaching (pp. 3-33). Mahwah, NJ: Lawrence Erlbaum Associates.

Lucero, M. (2003). Entre el trabajo colaborativo y el aprendizaje colaborativo. Revista Iberoamericana de Educación, sección lectores. Retrieved from  http://www.rieoei.org/deloslectores/528Lucero.PDF.

Matos, J. F., Alves, A. S., Rodrigues, C., Sousa, J. C., Dos Santos, M. P., Félix, P., . . . Ramos, V. (2003). Cultivating communities of practice within project weblabs. Challenges 2003: III International Conference about Comunication and Information Technologies on Education. Retrieved from http://www.lkl.ac.uk/kscope/weblabs/papers/Paper_Challenges03_portugal.pdf

Mor, Y., Noss, R., Hoyles, C., Kahn, K., & Simpson, G. (2006). Designing to see and share structure in number sequences. International Journal for Technology in Mathematics Education, 13(2), 65-78.

Mousoulides, N., & Philippou, G. (2005). Developing New Representations and Mathematical Models in a Computational Learning Environment. In M. Bosch (Ed.), Proc. 4th Conf. of the European Society for Research in Mathematics Education - CERME 4 (pp. 1061-1070). Barcelona: FUNDEMI IQS, Universitat Ramon Llull.

Noss, R., & Hoyles, C. (1996). The visibility of meanings: Modelling the mathematics of banking. International Journal of Computers for Mathematical Learning, 1(1), 3-31. doi: 10.1007/bf00191470

Papert, S. & Harel, I. (1991). Situating constructionism. In S. Papert & I. Harel & S. Papert (Eds.), Constructionism. N.J.: Ablex Publishing Corporation.

Papert, S. (1972). Teaching children to be mathematicians versus teaching about mathematics. International Journal of Mathematical Education in Science and Technology, 3(3), 249-262.

Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. N.J.: Basic Books, Inc.

Sacristán, A. I., Calder, N., Rojano, T., Santos-Trigo, M., Friedlander, A., Meissner, H. (2010). The Influence and Shaping of Digital Technologies on the Learning–and Learning Trajectories–of Mathematical Concepts. In C. Hoyles & J. Lagrange (Eds.), Mathematics Education and Technology-Rethinking the Terrain. The 17th ICMI Study (pp. 179-226). NJ: Springer.

Sánchez, J. F., Dormido, S., Aranda, J., & Ruipérez, P. (2002). Virtual control lab using Java and Matlab: A qualitative approach. IEEE Control Systems Magazine 22 (2), 8-20.

Schmid, C., Eikaas, T. I., Foss, B., & Gillet, D. (2001). A Remote Laboratory Experimentation Network. 1st IFAC Conference on Telematics Applications in Automation and Robotics. Robotica, 20(2): 449-454.

Sendova, E., Nikolova, I., Gachev, G., & Moneva, L. (2004). Weblabs: A Virtual laboratory for Collaborative e-learning. In C. D. Kloos & A. Pardo (Eds.), EduTech: Computer-aided design meets computer aided learning (pp. 215-221). Dordrecht: Kluwer Academic Publishers.

Simon, M. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26, 114–145.

Simpson, G., Hoyles, C., & Noss, R. (2005). Designing a programming‐-based approach for modelling scientific phenomena. Journal of Computer Assisted Learning, 21(2), 143-158. Retrieved March 17, 2012, from http://www.lkl.ac.uk/kscope/weblabs/theory.htm

Wenger, E. (1998). Communities of Practice: Learning, Meaning, and Identity. Cambridge: Cambridge University.