Constructionist learning of geometry

Valentina Dagiene dagiene@ktl.mii.lt

Faculty of Mathematics and Informatics, Vilnius University, Lithuania

Egle Jasute egle.jasute@gmail.com

Faculty of Mathematics and Informatics, Vilnius University, Lithuania

Abstract

This paper deals with a constructionist learning approach to geometry and particularly with dynamic geometry software. A theoretical framework of constructionism and its connection with geometry education is discussed. Dynamic geometry education is important for pupils to develop visualisation and spatial thinking. The reasons of usage difficulties of dynamic geometry and the way how to help mathematics teachers to use digital tools for constructionist learning are presented. The main attention is paid to the constructionist learning model for learning geometry developed by Baytak (2011). The model is extended and adapted for teaching geometry at a lower and upper secondary school level. The new features of learning and teaching mathematics are discussed. Finally, interactive books for teaching mathematics in secondary schools are presented and discussed. The example of practical usage of pre-created interactive sketch is presented.

Keywords

Constructionist learning, learning by doing, mathematics education, dynamic geometry

Introduction

"Constructionism shares constructivism’s view of learning as building knowledge structures through progressive internalization of actions... It then adds the idea that this happens especially felicitously in a context where the learner is consciously engaged in constructing a public entity, whether it’s a sand castle on the beach or a theory of the universe" (Papert, 1991, p. 1)

Seymour Papert launched the idea of constructionism more than a quarter of a century ago. The latter idea inspires to develop a theory of pedagogy that could foster learning. It is more than a methodology, seeking to develop knowledge structures in the mind of a child alongside physical or virtual structures external to the mind. Understanding the development of the structure of knowledge is part of a powerful pedagogic theory and practice. Constructionism is about the ways that human beings come to learn most effectively; building, debugging, sharing in ways that could at last be reasonably straightforward thanks to digital technologies.

Constructionism increasingly struggles into many areas of education. Mathematics, particularly geometry, is one of the most appropriate subjects for realizing constructionist ideas because geometry itself plays with objects and requires constructing them. This shows that learning geometry can be grounded by the constructive theory and based on teachers’ interaction ways to constructionist learning. We analyse the influence of the interactive tool on the teacher’s traditional methods of teaching, trying to answer a question how to help the traditional teacher to integrate digital tools and support the constructionist learning. We have extended and adapted the constructionist learning model to geometry developed by Baytak (2011).

The new psychological tendency and development of information technologies have affected the development of new technological tools to be used for active teaching and learning methods. The first ideas of constructionism based on information technology in education have been spread by S. Papert. He was one of the first who looked at a child as a creator (Papert, 1993). Most of the follow-up educational software developers relied on the S. Papert ideas and methodologies (Hay, Barabbas, 2001). We have argued that dynamic geometry software realizes constructionist ideas as it enforces a constructive approach.

Constructionist ideas can be effectively realized in mathematics education. However, it is still a strong focus on mathematical knowledge acquisition in Lithuania (Dagienë et al., 2007). Teachers are not prepared to accept a new view of mathematics education. After literature studies, we have found some reasons why most math teachers do not accept constructionist ideas (Hohenwarter et al. 2009; Stols et al., 2011). These studies have inspired some ideas: to develop some approach how to make mathematics studies easier for both students and teachers. The developed approach links together a traditional way of teaching mathematics with the facilities of new media. So, we have not to enforce traditional teachers for quick changes, but to offer them our help by developing flexible interactive tools with dynamic geometry which supported the mathematics curriculum. These tools allow appearing of the new features of learning and teaching mathematics: interactive sketches open way of new geometric visualisation and mathematical thinking, the students become active researches and developers, the creation of dynamic sketches develop students’ creativeness and deeper understanding of geometry and relation between geometry and algebra.

The developed interactive tool requires a new constructionist learning approach to mathematics education. We have proposed a model for learning mathematics with dynamic geometry in this paper. The proposed model is based on the Baytak (2011) model in combination with Kolb’s (2005) learning cycle.

The developed interactive tool is created using the dynamic geometry software, namely Geometer's Sketchpad (http://www.dynamicgeometry.com/). This program has been chosen for several reasons: first, it has been implemented in Lithuanian schools (it is localized, teachers are trained to use the program, materials for teachers training are prepared); second, Geometer's Sketchpad is able to create interactive books with dynamic sketches (using the same program without any additional program) and third, Geometer's Sketchpad sketches are based on the hierarchy of objects. Also there is possibility to create scripts and additional tools (Jackiw, 1993).

Theoretical framework

Constructionist learning

Education is affected by various psychological theories. For many years the training has been based on the ideas of behaviourism and focuses on the accumulation of knowledge, teaching lectures, and reflection. At the same time, other psychological tendencies have been developed, i.e. a cognitive theory which has changed the approach to teaching. Teaching ideas based on the collection, processing, development, attention is directed to thinking. Basically in both directions the teacher’s and student’s role is different: in the first one the teacher is a trainer and information provider, and the student is the receiver of information, in the second one the teacher is an advisor and the student is the information gatherer, handler and developer (Hubwieser, 2000).

The mathematics teaching was influenced by these two psychological theories. Therefore, the present-day mathematics teachers use quite a comfortable method which does not require a lot of preparation for teaching – lecture. Or otherwise, the teacher integrates cognitive ideas, methods, based on looking at the student as a thinking person: discussions, problem solving, and collaboration. Thus, both behavioural and cognitive methods of training are adequate when they match teaching and learning goals.

With an increasing number of information contents, the man just could not remember a superfluity of information. Thus, Jean Piaget's psychology-based training – constructivism – was used. The main principle of this theory is experience-based knowledge creation, where the learner is actively involved in teaching and learning. When shifting from teaching to learning, it means that the whole educational process focuses on learning, on new tools that encourage everybody to learn successfully and be motivated. The teacher becomes a counsellor who helps to strengthen the links between different areas of education.

Constructivist learning emphasizes the following ideas: 1) the children are developers of their own knowledge and external realities; 2) knowledge of the world is constructed and interpreted by using certain tools and symbols.

Seymour Papert (1993) looked deeper and wrote that it was important how children learn in a particular context, using their own and other’s created objects and he focused on the role of ICT in human learning. The new learning theory – constructionism – has begun, where the main point is to learn different methods and ways of purposeful information to select and absorb the abundance of knowledge, and using them effectively, to create new knowledge. A few years later, S. Papert (1999) outlined eight big ideas of constructionist learning: (1) learning by doing – students learn better when learning is part of doing something what is interesting; (2) technology as the building material – things can be made more interesting; (3) hard fun – to enjoy what you are doing; (4) learning to learn – student has to take charge of his own learning; (5) taking time – the proper time of the job – student have to learn to manage time himself; (6) you cannot get it right without getting it wrong – to goof in the way is nothing wrong; (7) do unto ourselves what we do unto students – to let students see us struggle to learn; (8) digital world – using computers to learn about everything.

A well known percentage of realized information using various teaching methods allows us look at the difference of effectiveness of teaching methods from a lecture to teach others (Brooks, 1993). The constructionist background of teaching methods is practice by doing and even 75% information is realized using these methods.

Other constructionist Richard Noss (2010) has presented features of constructionist learning: sharing, personalization, making learnable what is unlearnable, making visible what is invisible, and mastery. Baytak argues that the constructionist learning consists of two steps: the internal step – learning is an active process when students construct their knowledge from their experiences, and the external one, which is based on the research which suggests that students learn best by making artefacts that can be shared with others (Baytak, 2011). The internal step derives from constructivism, the external step relates to the constructionism.

Dynamic geometry and constructionism

The new psychological tendency and development of information technologies have affected the development of new technological tools for using active teaching and learning methods. The first ideas of constructionism based on information technology in education have been spread by S.Papert as mentioned above. He is the creator of the education technology, based on the constructionist idea – learning by doing. Most of the follow-up educational software is grounded by S. Papert ideas and methodologies (Hay, Barabbas, 2001).

One of such software is the dynamic geometry for teaching and learning mathematics. There are plenty of definitions of dynamic geometry, but they emphasize that the dynamic geometry is a technological tool that allows users to construct directly associated geometric objects of mathematical phenomena, that can be transformed and explored using a variety of technological and computerized management tools, and to hold relationships between designed objects at the same time. Most of the dynamic geometry software allows us to draw and construct Euclidean geometry objects and to transform (move, rotate, stretch or reflect) them, such as additional tools to animate drawings, to draw graphs of functions on the Cartesian or polar coordinates, write equations of straight lines and circles, to measure the geometric object by selected measurement units to perform various arithmetic operations, supplemented by drawings of the inscriptions, to write the mathematical text (Jasutė & Dagienė, 2011). Often such a constructed sketch is called as a dynamic or interactive image.

The fundamental of the dynamic geometry development bear a didactic idea to construct student’s knowledge by investigating geometric objects and relationships between them (Jackiw, 2004). Scientists improved the dynamic geometry influence on deductive thinking, mathematical thinking, mathematical imagination, geometric perception (Jones, 2000; Patsiomitou et al., 2008). Thus, learning by constructing is the main principle of dynamic geometry, and it can be realized so that the dynamic geometry implements all S. Papert’s constructionist learning ideas, mentioned in the introduction. Especially learning by doing is the basic idea of dynamic geometry software.

Following R. Noss (2010), the dynamic geometry enables us to personalize geometry learning: 1) each student can learn at his own rate, use his experience; 2) creation and pre-created sketches can be used for every learning style of Kolb’s experiential learning cycle (active hypotheses, active testing, concrete experience and reflective observation). Kolb’s learning cycle lies in the educational background of the dynamic geometry.

The fundamental idea of dynamic geometry lies in the idea of constructionism: students are learning by their own experience and sharing with others. The dynamic geometry is constructed for teaching and learning geometry (and sometimes for algebra) in such a way that it helps to use various methods of teaching and learning, to make the teaching process more attractive, and to learn geometry deeper. The dynamic geometry is designed so that the student is actively involved in the design and study.

Constructionist learning environment

Constructionist learning model of mathematics using the dynamic geometry

One of the well-known approaches to up to date learning geometry is presented by A. Baytak (2011). We have chosen the model and adapted it for learning mathematics using the dynamic geometry.

A. Baytak (2011) presents the model of constructionist learning, where he declares four steps: planning, designing, testing, and sharing. His model is constructed for learning by game design (Baytak, 2011). Internal learning and external learning have been distinguished. He ascribes the internal learning to constructivism and the external learning to constructionism.

When learning using the dynamic geometry, the design step is changed by developing a drawing scenario, and testing is changed by drawings. Other steps are left the same. The grey part outside the schema (Figure 1) is the Baytak model, and the black part is an extended model adapted for geometry learning using the dynamic geometry.

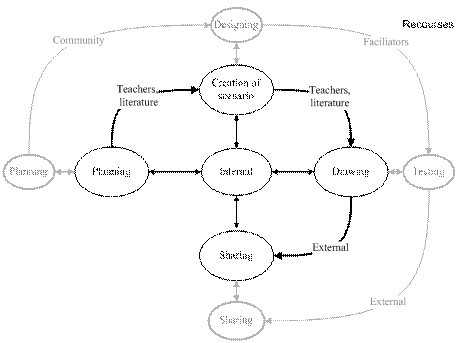
Figure 1.Model of the constructionist learning of geometry (the extended and adapted Baytak model).

In this model, a student is an active creator who shares his created sketch with other students. In this model, four stages for the student are seen: 1) planning – to get his task and start to plan how to realize it; all resources and teacher’s instructions can be used; 2) creation of its scenario – to think about the scenario how to draw a sketch (steps of drawing) – the algorithm how to draw a geometric object with pair of compasses and a ruler must be developed, the knowledge of geometry and the usage of dynamic geometry software are needed in this stage; 3) drawing – to create a drawing and test it by dragging free objects to verify whether the drawing is correct, and 4) sharing – to present and explain the drawing to other students; it can be discussed from the way how it has been created and how geometric correctness has been proved.

We used Kolb’s (2005) experiential learning cycle to explain our view of constructionist learning mathematics using the dynamic geometry. Kolb’s learning cycle is for experiential learning. Learning by dynamic geometry is based on students’ experience and practice. There are four stages in the experiential learning cycle: concrete experience, reflective observation, abstract conceptualization, and active experimentation. These stages are related with four learning styles: diverging, assimilating, converging, and accommodating. These relations are seen in Table 1.

Table 1. Kolb’s learning styles

Usually there are students with several learning styles in the class. Thus, a teacher has to prepare the material for all the learning styles for a lesson. In this case, we are interested in Kolb’s cycle learning stages for mathematics learning to make the learning process more effective, to involve most students in the class. To this end we have extended the model of geometry related to Kolb’s learning cycle stages (Figure 2).

Figure 2. The Extended Constructionist learning model

The model illustrates five steps of learning: 1) analyzing – a student moves free geometric objects in the pre-created sketch and observes what is moving, changing, what properties remain the same, etc.; 2) formulating – a student formulates concepts, properties, axioms, theorems according to his experience of dynamic drawings; 3) creating a drawing – when a student analyzes the drawing and gets some knowledge by his experience, he can create some drawing himself by the steps which have been described in Figure 2; 4) a student shares and discusses his drawing with other students; 5) creating models – here we mean that a student has to creates a model (plan, tile, etc.) of a realistic object (box, furniture, room, yard etc.) using dynamic geometry and he shares it, discusses his drawing with other students. In all steps the student constructs his own internal knowledge by interactions with the external learning environment (teachers, students, literature, internet etc.). The whole process is associated with the information technology (in our case, dynamic geometry software, internet explorer). These steps are new trend in teaching and learning mathematics. The student is involved in active process and interactive sketches open way of new geometric visualisation and mathematical thinking.

All five steps are related to Kolb’s learning stages as shown in Table 2.

Table 2. Relation of the learning steps to Kolb’s stages

Comparing Tables 1 and 2, each step of the model is attached to one of Kolb’s learning styles: analyzing and formulating to diverging; drawing to converging; creating models to assimilating and share to accommodating.

The developed model can be useful for teachers to prepare lessons. It probably can help to analyze the learning or teaching material and to think how to adapt it to different learners and to use constructionist mathematics learning. The first two steps of the model are adjusted for mathematics learning with dynamic geometry in this paper. The others steps requires more detailed studies.

Reason of creating pre-constructed sketches

Constructionist ideas can be effectively realized in mathematics lessons. However, there is still a strong focus on mathematical knowledge acquisition in Lithuania (Dagienë et al., 2007). Therefore constructionist ideas are integrated into the teaching of mathematics very slowly because teachers have to adapt to the new environment. Most of them have to spend more time for preparing. Teaching mathematics is mostly based on an academic approach – it is intended for the national school – leaving mathematics exam obligatory for almost every higher school. In view of that, the majority of our mathematics teachers can be considered as traditional teachers.

Some more reasons, why mathematics teachers do not use constructionist learning tools, i.e. dynamic geometry in their lessons, have been found by analyzing literature:

§  The lack of the skills in information technology has an impact on the use of dynamic geometry for most teachers (Stols, Kriek, 2011).

§  The dynamic geometry is relatively complex for a math teacher for several reasons: first, a dynamic geometry construction is based on a hierarchy and to construct a sketch, teachers must have (or acquire) new skills of developing algorithms and programming by geometry; second, most tools of dynamic geometry software are rather complex for the teacher (Hohenwarter et al. 2009).

§  Some scientists see quite the other problem of information technology. They argue that the usage of digital tools depends on the teacher’s disposition. If the teacher uses active learning and constructive methods of teaching, he/she is willing to use the dynamic geometry for teaching, if the teacher uses traditional teaching methods, he/she is not willing to use information technologies for teaching (Stols, Kriek, 2011).

While there are some problems of using the dynamic geometry, the software can help teachers to use a variety of constructionist teaching and learning methods. Four guided methods are defined for teaching mathematics with dynamic geometry which are related more or less with the ideas of construcionism: 1) a student is constructing dynamic sketches himself by his experience; 2) a student is analyzing individually geometric concepts and properties of geometric objects in the pre-created dynamic sketches with some instructions and directed questions; 3) a student is analyzing pre-created dynamic sketches with the teacher in the class, if the teacher uses the dynamic sketch to illustrate the explanation of geometry and 4) a student is learning by a pre-created book of dynamic sketches, when he has all the sketches that consistently illustrate all the topics of geometry and can analyze them individually (Dagienë & Jasutiene, 2007). All the learning methods described can be used with the model presented in Figure 2.

These studies have inspired the ideas how to develop an approach making the mathematics studies easier for both students and teachers. The developed approach links together a traditional way of teaching mathematics with the facilities of uptodate media. Thus, we are not going to force teachers for quick changes, vice versa we offer them support by developing flexible interactive tools for dynamic geometry.

Interactive book with dynamic geometry

In order to find an effective and quick solution the educational mathematics program has been reviewed and dynamic drawings sets have been created for 9th and 10th grades (Dagienë, Jasutiene, 2006). More than 500 dynamic sketches have been created and put in the interactive book which makes it easier for teachers to prepare for mathematics lessons. The interactive books include a user-assistance, research directions and theoretical insertion, and additional tasks.

The interactive book can be used at classes in different ways: as the aids; students can explore drawings independently after lessons: students can use it while working individually and collectively; a teacher can to demonstrate and explain the topics of geometry much easier with the help of the interactive book. As shown in practice, the students like it more, when they can change a drawing and look what happens. Students feel then as researchers.

The interactive books compel teachers to think in advance what, when and how to present to students. For example, in the classroom with multimedia projector pre-created sketches can be used for a few minutes to illustrate one or more dynamic drawings.

If students are taught in the computer classroom and they are exploring drawing themselves, it is important to formulate the goals what teacher would like to teach, to prepare purposive questions for students, to which they seek answers and formulate their own concepts or draw conclusions. Such lessons in the computer classroom are very useful, because the opportunity for students to press the buttons themselves, discover themselves and to detect patterns, being moved by curiosity, to formulate their own questions and find their own answers of a great value.

It would be great, if students could use the interactive books in the lessons and after them. Then the teacher can give students a brief individual task or, over a longer period of time, a group task. The tasks can be related to the theoretical material and the textbook of the task.

Only some possible scenarios of teaching and learning with interactive book are reviewed in this paper. The innovative teacher can offer much more methods for effective mathematics learning and teaching in the class. The interactive book is used for first two steps of the Extended Constructionist learning model of learning mathematics.

The example of practical usage of pre-created dynamic sketch

An example of the usage of dynamic sketches is presented. It illustrates the possible way of learning of 10th grade topic “The function f(x) = ax³”. According to the Lithuanian national mathematics curriculum a student should to recognise graph of the function, to draw graph of the function, to calculate values of the function when learning this topic.

For this topic one dynamic sketch have been developed (Figure 3). It has been created considering the student skills what have to be developed by national curriculum. This sketch can be analyzed in four stages:

§  When student opens sketch he gets graph of function f(x) = ax³ with additional buttons on the screen. The student can change parameter a by pressing button “Change a” and look how the graph of the function is changing. He can notice how graph of function f(x) = ax³ look and where it is plotted when parameter is negative or positive number etc. From the other hand he can move point x on the axis and look what value function gets.

§  When student presses button “Show table” he gets additional information – table of values of function. He can analyze values of the function in the table. The student can change parameter a and look what happen with the values in the table.

§  When student presses buttons “Show y=x³” and “Show y=-x³” the two more graphs are plotted in the coordinate system and two additional lines appear in the table of the values. The student can compare three graphs and values of all three functions.

§  When student presses button “Show conclusion” the some theoretical statements appear. The student can test himself if his acquired skills are correct.

While some instructions and additional tasks are given in the interactive book with this sketch it is recommended the teacher to prepare consistent questions, instructions or worksheets for students’ independent or group work. Practice shows that these instructions help students to concentrate on acquiring correct skills which have to be developed.

  

Figure 3. Example of the investigation of function f(x) = ax³ with the interactive book for 10th grade.

The analysing of such pre-created sketches has more potency than teaching with traditional methods for some reasons:

§  When the function f(x) = ax³ is investigated in the class, only few examples of such function can be provided in the textbook, notebook, or on the board. With an interactive book, in a few minutes all the properties of function f(x) = ax³ and changes in the graph can be easily seen (Figure 3).

§  This sketch illustrates relationship between the graph and the expression of its function directly. This skill is not mentioned in the curricula, but it is hidden under the calculation of values of the function.

§  The students are active researches in this process ant it is more important feature in the constructivist learning.

§  Pre-created sketches do not require additional teachers’ skills and can be easily adjusted for class.

This example illustrates only one possible scenario of a lesson when student actively analyzes sketch. This sketch can be used in the teaching scenarios which where discussed above and can be creatively used in other scenarios.

Conclusions

The information technology opens a way to constructionist learning in mathematics. Using the information technology in the classroom, a teacher has to change the traditional approach to teaching and learning methods. In order to achieve better learning and relationships with students, the teacher has to apply innovative approaches or to integrate them into traditional ones.

We have extended and adapted constructionist learning model for geometry learning using the dynamic geometry. This model allowed us to conceive constructionist learning of mathematics more clearly. A student who has passed all the steps of the model, gains deeper understanding of the real world and relations of algebra with geometry, which is very important for student’s mathematical thinking and learning motivation. However, these statements must be proved by some experiments in the future.

The computer program Geometer’s Sketchpad and created dynamic sets of drawings “Mathematics with Dynamic Geometry“ for the 9th and 10th grades are appropriate for mathematics education by constructionist ideas. The student is an active learner and the teacher becomes a counsellor and consultant for the student when dynamic geometry is used. In addition, the student can use dynamic sketches independently of the teacher and his IT competence, because interactive books have user support, advice, and theoretical insertion. In this case, the teacher can only give advice to students about mathematical issues (what he is doing in the traditional math classes).

The presented model and interactive tool open new tend to mathematics education. The student become active researcher and developer and the teacher become adviser for student. The pre-created interactive sketches deliver new view of geometry visualizations: with an interactive sketch all the properties of the geometric or algebraic objects can be investigated in a few minutes whereas the traditional methods allow investigating of few examples of such objects provided in the textbook, notebook, or on the board.

References

Baytak, A. (2011). An investigation of the artefacts, outcomes, and processes of constructing computer games about environmental science in a fifth grade science classroom. Phd Thesis. BiblioLabsII, 2011. ISBN-13: 9781243722775

Brooks, J. and Brooks, M. (1993). In Search of Understanding: The Case for Constructivist Classrooms, ASCD

Dagienë V., & Jasutiene, E. (2007). Visualization and exploring mathematics using information technologies. Information Sciences (2007) Vol. 41

Dagienë V., & Jasutiene, E. (2004). Teaching and learning mathematics with Geometer‘s Sketchpad, Lithuania mathematics XIV conference.

Dagienë V., & Jasutiene, E. (2006). Developing Dynamic Sketches for Teaching Mathematics in Basic Schools, The 17th ICMI (International Commission on Mathematical Instruction) Study: Technology Revised, Hanoi University of Technology, Vietnam, (p. 120–127).

Dagienë V., Jasutiene, E., & Jevsikova, T. (2007) An Approach to Combine Learning Entities to Support Mathematics Curriculum in Schools. In: D. Benzie, M. Iding (Eds.) Informatics, Mathematics and ICT: a "golden triangle". CD proc.: Working Joint IFIP Conference. Northeastern University, Boston, Massachusetts, USA, June (p. 27–29), 2007.

Hay K. E.& Barab, S. A. (2001). Constructivism in Practice: A Comparison and Contrast of Apprenticeship and Constructionist Learning Environments, The journal of the learning sciences, 10(3), (p. 281–322), Lawrence Erlbaum Associates, Inc.

Hohenwarter, J., Hohenwarter, M., & Lavicza, Z. (2009). Introducing Dynamic Mathematics Software to Secondary School Teachers: The Case of GeoGebra. Journal of Computers in Mathematics and Science Teaching, Vol. 28, (p135-146) Apr 2009

Hubwieser, P. (2000). Didaktik der Informatik. Grundlagen, Konzepte, Beispiele, Springer.

Jasutė E., Dagienė V. (2011). A Model of Interactive Geometric Visualization with Dynamic Geometry. Information Sciences 2011 Vol. 56. ISSN 1392-0561

Jasutė E., Jasutiene, E. (2007). Constructive methods of mathematics teaching, Lithuania mathematics collection, Vilnius university, no. 47, 2007, 233 p.

Jones, K. (2000). Providing a Foundation for Deductive Reasoning: Students' Interpretations when Using Dynamic Geometry Software and Their Evolving Mathematical Explanations, Educational Studies in Mathematics 44: (p. 55–85), 2000.

Kolb, Y., A. (2005). The Kolb Learning Style Inventory – Version 3.1 2005 Technical Specification. (http://www.whitewater-rescue.com/support/pagepics/lsitechmanual.pdf)

Laborde, C. (1998). Visual phenomena in the teaching/learning of geometry in computer-based environment, Perspectives on theTeaching of Geometry for the 21st Century. An ICMI Study: Kluwer Academy Publishers, Netherlands, (p. 113-121).

Miller, N. (2006). Visualization in cones and pool tables using Geometer‘s Sketchpad. Problems, and Issues in Mathematics Undergraduate Studies. West Point. Vol. 16, p. 257, 18 psl.

Neuburg, R. & Harris,V. (2003). How am I learning? Kaunas: Technologija, (p. 17-21).

Noss, R. (2010). Reconstructing Constructionism. Constructionism 2010, Paris. CD proc.

Olkun, S., Sinoplu, N.B. & Deryakulu, D. (2009) Geometric Explorations with Dynamic Geometry Applications based on van Hiele Levels, International Journal for Mathematics Teaching and Learning

Papert, S (1991) Preface, In: I. Harel & S. Papert (Eds), Constructionism, Research reports and essays, 1985-1990 (p. 1), Norwood NJ

Papert, S. (1993). Mindstorms: Children, Computers, and Powerful ideas. Da Capo Press. 1993

Papert, S. (1999) The Eight Big Ideas Behind the Constructionist Learning Laboratory. In Stager, G. An Investigation of Constructionism in the Maine Youth Center. Doctoral dissertation. The University of Melbourne. 2006.

Patsiomitou S, & Koleza E. (2008). Developing students geometrical thinking through linking representations in a dynamic geometry environment. International Group for the Psychology of Mathematics Education. Proceedings of the Joint Meeting of PME 32 and PME-NA XXX, Vol. 4, July 17-21, 2008, (p. 89 – 96)

Stols, G. & Kriek, J. (2011). University of South AfricaWhy don't all maths teachers use dynamic geometry software in their classrooms? Australasian Journal of Educational Technology, 2011, 27(1), (p. 137-151)