Differential approximation of a cylindrical helix by secondary school students

Ioannis Zantzos, izantzos@math.uoa.gr

Educational Technology Lab, School of Philosophy, University of Athens

Chronis Kynigos, kynigos@ppp.uoa.gr

Educational Technology Lab, School of Philosophy, University of Athens

Abstract

Some of the findings of a research study referring to two third grade secondary school students’ attempt to design the shortest path between two points on a cylindrical surface are presented in this paper. The students worked using a 3d Logo / Turtle Geometry environment (MaLΤ) which combined the dynamic manipulation of mathematical objects with the symbolic notation by means of the Logo programming language. The research findings showed that the microworld designed can form the basis for studying notions of the conceptual field of curvature in space at least at an intuitive level with the students developing meanings of notions such as curvature, torsion and isometry in space.

Keywords

Curvature, differential approximation, helix, shortest path

Introduction

 One of the basic problems in geometry is to define those geometric objects which allow us to differentiate one geometric object from another or to know when these objects are the same. For example, line segments are defined according to their lengths and triangles through the knowledge of their sides (Congruent triangles postulate). Similar problems are proved to exist in the case of regular curves both in plane and in space in general. In particular, the curve is defined in an one and only way (apart from its position in space) by two functions of its arc length: curvature and torsion (Lipschutz, 1969). The notion of curvature is one of the central concepts of differential geometry; one could argue that it is the central one, distinguishing the geometrical core of the subject from those aspects that are analytic, algebraic, or topological (Osserman, 1990).

The notion of curve, the study of its properties and of the ways it can be approached consist one of the most important issues in third level education; as, for example, in differential geometry. The extremely difficult formalism as well as the complicated formulas required consist a significant obstacle so that these notions and differential geometry in general can become approachable to many a student. (Henderson, 1995; Kawski, 2003). Nevertheless, the notion of curve and notions related to it are met in 2nd level education syllabuses which, however, seem to focus on its various properties rather than on the notion of the nature of the curve as contrasted with straight line. For instance, they are met in polygonal approximations of curves, the measurement of the length of a circle and circular arcs, the measurement of the area of circular disc as well as in the study of the convexity of a function since the second derivative measures concavity, a curvature- type measurement. Similar approximating procedures can be applied in cases when, for example, the area and the volume of a cone are calculated. Curvature also plays an important role in physics. The magnitude of a force requires to move an object at constant speed along a curved path is according to Newton’s laws, a constant multiple of the curvature of the trajectory.

The appearance of dynamic digital environments and especially of 3D spatial environments seems to make the scenery change. The ability to scrutinize and the dynamic manipulation digital technology provides nowadays can a) firstly, enable students to acquire experiences in such abstract notions generally in space, at least at an intuitive level before they reach the complicated formulas of differential geometry b) secondly, intervene in the transition from the intuitive level to the theoretical level (Jones 2000) c) thirdly, enable us to restructure domains (Wilensky, 2010). Especially through the use of the turtle geometry and its graphics we are given the ability to approach curves in an alternative and broader way.                                                            

The turtle approach enables us to turn to the real geometrical definition of the curves and develop representations which are often clearer and closer to the authentic definition (Loethe, 1992). According to Yerushalmy, M and Schwartz, J.L (1999), students by means of suitable digital tools engaged themselves in the study of a number of notions facing the problem of the study of the curvature of a level function reaching a high level of abstraction and an even deeper level of understanding. Researches have also shown that even young students can develop meanings such as curvature in plane when they engage themselves in suitable computational environments which combine the logo programming language and the dynamic manipulation of geometric objects. (e.g Kynigos and Psycharis, 2003).

 In the unit below we are presenting the basic elements of the method we have implemented in order to approach notions of the conceptual field of curvature in space which is based on notions which can be met in any book of differential geometry ( e.g Aleksandrov, et al, 1969; O’ Neil, 1997). Then we ‘interpret’ the way of designing a curve in space through turtle movements.

The ‘Local Turning and Twisting’ method (LTT)

 A curve in space can be regarded as the path of a moving particle and can be defined by the Frenet-Serret frame movement which consists one of the most important tools in order to analyses a curve in differential geometry. The Frenet-Serret frame {T,N,B}, where T is the unit tangent vector, N is the principal normal vector and B is the binormal vector, provides a local orthonormal coordinate system at each of its point. The T and N vectors define a plane which called osculating plane of the curve at this point. The role of osculating plane is similar of that of the tangent that is for an area very close to a point the osculating plane is that plane situated close to the curve than any other. The place of the osculating plane changes from point to point along the curve. Obviously, if the osculating plane does not change, we have a level curve and it coincides with the osculating. The rotation of the frame as it moves is given by curvature and torsion. Exactly as the rate of change of direction of the tangent is characterized by curvature, so is the rate of change of direction of the osculating plane characterized by the curve torsion. Below we refer to the strict definition of curvature and torsion more analytically so that the approximation we are going to implement by means of the turtle geometry is more understandable.

Let A and M be two points of a curve close to each other with arc length Δχ. Let Δφ be the angle between the tangents at these points. The average range of change of direction will be Δφ/Δχ. Then the limit of the ratio Δφ/Δχ is defined as the curvature of the curve at the point A. Thus, the curvature is defined by the formula:   

The tangent has an important geometric property: near the point of tangency the curve departs less from this straight line than from any other. So, the distance from the points of the curve to the tangent is small in comparison with their distance from the point of tangency. Consequently, a small segment of the curve can be replaced by a corresponding segment of the tangent with an error that is small in comparison to  the length of the segment.

In addition, it is known (differential of a function) that when Δχ becomes small enough the numerator of the quotient of formula (1) become almost equal to the product k*Δχ. So, we can by approximation claim that a Δχ small arc of a curve can be replaced by its tangent and the angle between the tangents at two successive points is given by the formula:Δφ=κ*Δχ, where κ is the curvature at this point. Proportional things apply to torsion but now Δφ is the angle between the osculating planes at neighboring points and it is proven that torsion measures the rotation of the osculating plane round the tangents.

By now using the metaphor of the turtle, the plane the turtle is on each time reflects the osculating plane of the F-S frame and the straight movement of the turtle consists the direction of the tangent of the curve. Let A and B be two successive positions of the curve for front movement Δχ. We can assume that the turtle at its initial position has the direction of the tangent at that point. In order this part to consist by approximation part of the curve we want the turtle to cover, the commands we are going to give to it have to reflect the movements of the F-S frame at two successive points which movements, according to the fundamental theorem of Differential Geometry, are defined by curvature κ and torsion τ. That is, the turning of its straight movement  Δφ degrees on its plane determines curvature and the rotation round the straight line of its movement determines torsion. So the F-S frame movements are equivalent to the following movements of the turtle:

·        Twisting around its direction of movement, that is : lr(:κ*:Δx) 

·        Turning in its plane, that is: lt(:τ*:Δx)  and

·        Moving forward  Δχ,  that is:  fd(:Δx)

In addition, through the ability we are given by the software we are using to dynamically change Δχ we can have the desirable approximation by means of the tangents of the curve. If we combine the aforementioned with the Logo language commands, such as repeat or make or a simple recursion, we can have the graphic representation of any normal curve in space with satisfactory precision.

For a second alternative approximation we can by integration precisely calculate the angles where the turtle has to turn for a ‘local turning and twisting’ since curvature and torsion are rates of change. For example, it is proven that a conical helix has a curvature and torsion which are functions of the length of the arc by the formulas:  κ=400/s, τ=40/s.  By integrating, we are given the angles for a ‘local turning and twisting’:

 

The theoretical frame

 Vergnaud (1988), introduced the notion of conceptual field as a set of situations the mastering of which requires mastery of several concepts of different natures. He claims that “a single concept does not refer to only one type of situation, and a single situation cannot be analyzed with only one concept” (p. 141), and he argues that teachers and researchers should study conceptual fields rather than isolated concepts. Thus, on the basis of the aforementioned it is meaningless to study, in the frame we are referring, the notion of the shortest path between two points on the surface of the cylinder on its own. We assume that the aforementioned notion belongs to the conceptual field of ‘curvature in space’ as the notions, for example, of rate of change and arc length which are involved in the procedure of designing a curve based on the polygonal approximation by means of its tangents, are directly related to the notions of curvature and torsion in space.

With our basic aim being to examine the meanings the students develop in relation with the notions of differential geometry we planned activities based on the learning theory through constructions (constructionism, Kafai and Resnick, 1996). A main characteristic of the method which we considered to be suitable in this particular case was to provide them with a half-baked microworld to start with (Kynigos, 2007) under the name of the ‘shortest path’. A half-baked microworld is software designed in such a way that it challenges both teachers and students to decompose them, change or even construct something with them. They do not consist ready environments to be comprehended by teachers and then be used by students. They incorporate various notions and offer the students the basis to interact with the microworld. They aim to serve as starting points and the user to be acquainted with the ideas hidden behind the procedure of their construction.

The computational environment

The computational environment we used in our present research is MaLT (Kynigos, C. & Latsi, Μ. 2007), (http://etl.uoa.gr) which integrates symbolic notation- by means of Logo programming language- and the dynamic manipulation of mathematical objects. It is an expansion of the turtle geometry of the ‘Turtleworlds’ in 3d geometric space suitable for the construction and exploration of geometric objects. The turtle movements are determined by following commands: fd(:n) and bk(:n) which command the turtle to  take steps forwards or backwards, lt(:n) and rt(:n) move the turtle n degrees to the left or the right in its plane (osculating plane), dp(:n) and up(:n) turn the turtle upwards or downwards and rr(:n) , lr(:n) move the turtle around its axis. The basic tools of MaLT are (figure 1) the uni-dimensional variation tool (1DVT) which enables the user to dynamically manipulate the values of variables in a represented object and the 2d variation tool which is a two dimensional orthonormal system and is used to determine the co-variation of the values of two variables. An additional characteristic is its 3d Camera Controller which gives students the ability to dynamically manipulate the camera by means of the active vector and observes the object in the simulated 3d space from any side and direction he/she wishes. We should also point out the ability the user has got to insert ready-made 3d objects, such as a sphere or a cylinder, in a 3d virtual space and dynamically manipulate them.

Figure 1: The environment of MaLT

The Problem

The students were given the following problem:

‘Calculate and design the shortest path between two points on a cylindrical surface’.

 The students were told that they were allowed to use any materials they liked (for example, paper and scissors) and the following half-baked microworld under the name the ‘shortest path’:

to shortestpath :n :s :dx :c

repeat :n  [lr(:s)  lt(:c)  fd(:dx)]

end

The aforementioned microworld comprises a program with four variables each of which express the following: n expresses a number of repetitions, s expresses the turning of the turtle around the directions of its path (it defines torsion), dx defining the length of the turtle step and c defining the turning of the turtle in its plane (osculating plane) which in turn defines curvature. The execution of the aforementioned code produces a polygonal line (either in space or in plane, Figure 2) or a straight line. But in the case when dx is considered to be too small (it tends to zero) three kinds of curves can result from the aforementioned microworld which virtually represent the geodesic of the cylinder.

For s=0 and c=0 line segments

For s=0 and 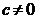 , circles arcs

For  και 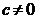 , helixes.

Our students were informed that this program would enable them to work out the way they could design such a path and that, at the end, they themselves could use it in order to construct their own models.

 

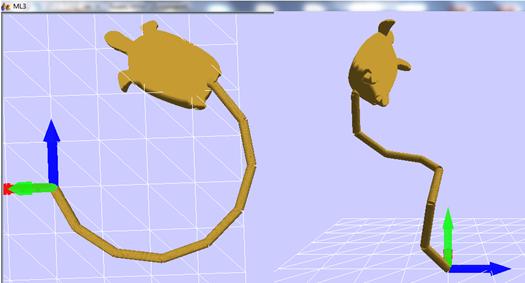
 Figure 2: Polygonal lines both in plane and in space

The Method

The present research is a design-based research method (Cob et all., 2003), which consists part of a broader research, with the participation of two 3rd  grade secondary school students and which lasted 19 hours. These particular students had already been familiarized with constructions in the logo programming language in the turtleworld environment. A video camera was used to record data and a sound and picture software (HyperCam 2) enabled the researcher to record the students’ actions and the conversations amongst the participants. In order to analyze the students’ mathematical thinking we were interested in the ways the students interacted with the available components of the software and in the ways they constructed mathematical meanings. At this point, we regarded the theory of situated abstractions, which enabled us to describe how the students construct mathematical meanings based on the functions of the particular software they were using and on the conversations between them, as extremely useful (situated abstractions, Noss & Hoyles, 1996). Another point we also focused on was how the students were trying to change the functionalities of the ‘faulty’ microworld they were given aiming to produce a different artefact which automatically give a helix with the shortest length (instrumentalization, Guin and Trouche, 1999).

 The results

The role of tangible tools

Although the students at first turned to the software they had been given in their effort to give an answer, they soon realized something else should be done. They decided to use the tangible objects, that is the paper the pen and the scissors, they had also been given. By rolling the paper up into a cylinder, they came to the conclusion that it would be enough to assume two points on the cylinder which would belong to the same generator and would be on the cylinder bases. The designing of a line which would join them (apart from the straight line) would be the solution. Upon unrolling the cylinder they noticed that the line which was formed  would be a straight line on the plane (geodesic in plane) but when they re–rolled up the cylinder a helix was formed. Nevertheless, this conclusion, although it seemed to be the solution, did not seem to satisfy the students at all.

S1: If we could suppose that the cylinder opens, then okay it is a straight line

S2: But if the cylinder could not open? (Meaning: then how could we design the helix?)

The conclusion the students came to through the above experimentations is that the curve in demand is a helix. The designing of such a curve though without the use of tangible materials, and the ability to generalize such a procedure demand the use of differential geometry notions which reflect the Frenet-Serret frame movement in space. The students appear to realize the limitations of tangible materials, and the inability to generalize the procedure in situations when their use is impossible.

Finding the way to design the helix by using the turtle

The aforementioned students’ speculation stimulated the researcher to impel them to use the software and the half–based microworld they had already had at their disposal. The students chose to insert a cylinder –out of the ready-made objects -of a 2.1 radius and a 5.54 height and by using the variation tools they tried to achieve the construction of a helical line which twisted round the cylinder with its two ends being the ends of the generator of the cylinder. Their initial suppositions referred to values which, although they seemed to have achieved their goal (that is the helical line to twist round the cylinder), the use of the camera proved wrong. Thus, from that time on each and every attempt of theirs initially comprised finding the values for n, c and dx with the simultaneous use of the camera and change of the values of the variables.

At their first correct attempts (with dx=1), they came to the following values: n=14, c=25, s=5 and dx=1. Although they seemed to be satisfied with the result of their experimentations, they continued to experiment after the following questions on the researcher’s part:

R: Is this a helix? (They play with the camera, zooming in on the screen at the same time)

S1: They look like lots of straight lines  (they are referring to the line segments which the helical line is composed of and with the execution of the half –based microworld provides them with)

R: What can you do so that you can turn it into a helix?

S1: Eliminate the angles

R: How can you eliminate the angles?

S1: If we decrease dx, let’s say to 0.1

S2: If we multiply it by ten [and then in the application he divides it by ten]

But the execution of the code with dx decreased demands a simultaneous change of the values of the other variables, c and s. And that is because, by changing dx and replacing it with a smaller value, a helical line is produced but it is not in accord with what they are expecting. This mainly occurs due to the following reasons: Firstly, the helical line does not twist round the cylinder they had inserted (the initial position of the turtle plays a significant role here but at the same time the values of c and s are such that at least graphically do not affect it) and secondly, it does not produce the shortest path (since if dx is replaced by a smaller value, a line of a shorter length is produced). After they have put down the values in their worksheets, they come to the conclusion that as dx takes smaller and smaller values we are given a line which looks like a helix with a length constantly decreasing and that the ratios c/dx and s/dx remain invariant and equal to 25 and 5 respectively. In fact, the rate of change of directions of the segments the turtle is moving on (the tangent) and its plane (the osculating plane) which define the curvature and the torsion of the curve respectively remain invariant. The replacement of the ratios they discovered in their initial code provides them with the corrected code and the solution in demand as it shows in figure 1:

to shortestpath :n :dx

repeat :n [lr(5*(:dx))  lt(25*(:dx))  fd(:dx)]

end

Then the researcher asks them:

R: Which values provide us with the helix we are looking for?

S1: The smaller dx is the better.

 The student seems to realize that the solution they are looking for does not only consist of the above code for specific values of the variables but it should also combine a limited procedure for dx. In fact, this procedure produces the correct helix only when

3D Reflection about a plane

After the students had successfully designed the shortest path, the researcher asked them if there were more helixes to the same cylinder which get again gave the shortest path between the two points. The students started to experiment using the variations tools and the camera and by now examining a variety of combinations of values, both positive and negative, they came to various conclusions which were related to the notions of isometry and orientation in space. The case when the students ‘came across’ the notion of isometry is characteristic. Whereas they had a helical line with values c=3 and s=0.06 their experimentation with the aid of the variation tools led them to the values c=3 and s=-0.06 which virtually gave them a symmetrical helical line for the xz plane. It is a reflection about xz plane, and the two curves twist in opposite ways (if the first is ‘right- handed’, then the second is ‘left-handed’) since both helixes have the same curvature and opposite torsion (a fundamental theorem of differential geometry).

R: These figures (he means the one where c=3 , s=0.06 and the other one where c=3 and s=-0.06) are different? If so, what are they different in?

S1: Substantially, they are exactly the same helixes.  They are identical but they have the opposite direction

S2: It looks as if we had a helix which reflects in the water 

Conclusions

The purpose of the present research was dual: Firstly, to study the degree to which this particular microworld could form the basis for the study of notions of the conceptual field of curvature in space by young, second level education students and secondly, to study the meanings developed by these particular students in their attempt to design the shortest path between two points on a cylindrical surface. The computational environment used in this research along with the LTT method helped students to express mathematical meanings for a number of notions of differential calculus  (for example, rate of change) as well as of differential geometry (for instance: curvature, torsion, geodesic and isometry) which has been shown to be notions difficult to be approached by even math students. One of the major advantages of the method applied is the fact that, not only were students able to visualize the Frenet–Serret frame movements (the role of which was replaced by the turtle) but the students were also given the ability to study, explore and symbolically represent these movements (by means of Logo) which are not easily achieved in dynamic geometry environments (DGEs). In this way, even young students are given the ability to engage themselves in notions of the conceptual field of curvature in space, at least at an intuitive level, before they reach notions of differential calculus and the complicated formulas of differential geometry. Although the way they used to design the helix does not tally with the strict formalism of differential geometry, the answers the students came up with are indicative of the fact that a restructuration (Wilensky, 2010) of the notion of curve based on its polygonal approximation is feasible in secondary education.  

References

Aleksandrov, A., Kolmogorov, A., and Lavrent’ev, M. (1969), Mathematics: Its Content, Methods, and Meaning, Vol. II (2nd ed.), Cambridge: MIT Press,

Cobb, P., Confrey, J., DiSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, Vol. 32-1, 9-13.

Guin, D. and Trouche, L. (1999). The complex process of converting tools into mathematical instruments: the case of calculators. The International Journal of Computers for Mathematical Learning 3(3): 195–227.

Jones, K. (2000). Providing a Foundation for Deductive Reasoning: students’ interpretations when using Dynamic Geometry Software and Their Evolving Mathematical Explanations. Educational Studies in Mathematics, 44 (1-2), 55-85.

 Henderson, D (1996). "Alive Mathematical Reasoning", Proceedings, Annual Meeting of the Canadian Mathematics Education Study Group, Halifax, NS: Mount Saint Vincent University Press, 27-33,

Kafai, Y. and Resnick, M. (eds.) (1996). Constructionism in practice: Designing, thinking and learning in a digital world.  Lawrence Erlbaum Publishers, Mahwah

Kawski, Μ (2003). Curvature for everyone. 8th Asian Technology Conf Math, Hsin-Chu, Taiwan 2003,

Kynigos, C. (2007). Half-Baked Logo Microworlds as Boundary Objects in Integrated Design, Informatics in Education, 2007, Vol. 6, No. 2, 1–24, Institute of Mathematics and Informatics, Vilnius

Kynigos, C. & Latsi, Μ. (2007). Turtle’s navigation and manipulation of geometrical figures constructed by variable processes in 3d simulated space. Informatics in Education, Vol. 6, No. 2, 359-372.

Kynigos, C., & Psycharis, G. (2003). 13 year-olds meanings around intrinsic curves with a medium for symbolic expression and dynamic manipulation. In N. A. Paterman, B. Dougherty, & J. Zilliox (Ed.), Proc. 27th Conf. of the Int. Group for the Psychology of Mathematics Education (Vol. 3, pp. 165–172). Honolulu, Hawaii, U.S.A: PME.

Lipschutz, M. M. (1969). Theory and Problems of Differential Geometry (Schaum’s Outline Series). New York: McGraw-Hill

Loethe H., (1992). Conceptually Defined Turtles, in: (Hoyles, D. and Noss, R. eds.),Learning Mathematics and Logo, The MIT Press,

Noss,R., & Hoyles, C. (1996). Windows on mathematical meanings. Dordrecht, The Netherlands: Kluwer

O’Neill ,B.(1997) Elementary Differential Geometry, Second Edition.Academic press

Osserman, R. (9990). Curvature in the eighties. The American Mathematical Monthly, Vol. 97, No. 8, Special Geometry Issue, pp.731-756.

Vergnaud, G. (1988). Multiplicative structures. In J. Hiebert & M. Behr (Eds.), Number concepts and operations in the middle grades (pp. 141-161). Hillsdale, NJ: Lawrence Erlbaum Associates.

Wilensky, U. (2010). Restructurations: Reformulating knowledge disciplines throw new representational forms. In J. E. Clayson & I.Kalas (Ed), constructionism 2010 Paris, France

Yerushalmy, M., Schwartz, J.L. (1999) A procedural approach to exploration in calculus.

International Journal of Mathematical Education in Science and Technology, 30 (6), 903-

914.