The Continuing Story of the Painless Trigonometry Projects: Eratosthenes’ method and the Parthenon

Ana Isabel Sacristán, asacrist@cinvestav.mx

Dept. of Mathematics Education, Cinvestav, Mexico

Jesús Jiménez-Molotla, jj_molotla@hotmail.com

Esc. Secundarias Diurnas “L. Yivkova” T. Mat. “J. E. Rodo” T. Vesp., DF, Mexico

Abstract

In this paper we continue the on-going story of the Painless Trigonometry projects in Mexico that we have presented at the past two Eurologo/Constructionism conferences (Jiménez-Molotla et al., 2007; Jiménez-Molotla & Sacristán, 2010). These are long-term, interesting, constructionist projects were students become engaged and motivated, while they learn many mathematical topics in the official syllabus in a fun and meaningful way, but also have early access to other “powerful ideas” (Papert, 1980), that is, “advanced” mathematical concepts, such as trigonometry that usually are not considered for students of the age-groups we work with (12-14 years-old). The main project presented was inspired by the host country of Constructionism 2012: building a model of the Parthenon, and along the way, we also engaged in another Greek-related project: the measurement of the Earth using the method of Eratosthenes.

Keywords

Mathematics; Trigonometry; 3D geometry; school project; Logo

Introduction

At Eurologo 2007, we reported our first long-term “Painless trigonometry” project (Jiménez-Molotla et al., 2007), and then in Paris, we presented an evolution of the previous projects: the “Eiffel tower project”, inspired by the host city for Constructionism 2010. In Paris, we were asked if, for the conference in Greece, we would call our next project “The Parthenon”, in honour of the new host city, and so we started thinking about this. We have spent the last two years working on this idea. Along the way, we also had the opportunity to engage in another “Greek venture”, when we participated in a project to measure the Earth’s radius using the method of Eratosthenes. Thus, in this paper, we present this year’s work, which, appropriately for this conference, includes the work of two great Greek mathematicians, Pythagoras and Eratosthenes, as well as the construction of a model of the iconic Greek Parthenon.

Background and theoretical framework

As presented in our previous papers (Jiménez-Molotla et al., 2007; Jiménez-Molotla & Sacristán, 2010), in 2001-2002, the junior secondary school where Jesús (co-author of this paper) and his colleague Alessio teach, incorporated the Mexican, government-sponsored “Teaching Mathematics with Technology” (EMAT) program. That program promoted a constructivist use of open software tools (‘open’ in the sense of changeable; ‘tools’ in the sense that they help accomplish educationally relevant tasks – di Sessa, 1997) and therefore wanted students to be in control and have decision power on how to use the software; the tools in EMAT thus included Spreadsheets (Excel), Dynamic Geometry (Cabri-Géomètre), and Logo (MSWLogo). That program provided the foundation for the future work in that school, in technology-based mathematical activities and projects: since around 2005, Jesús has worked in developing interesting constructionist (Harel & Papert, 1991) long-term mathematical projects with an integral use of technological tools like EMAT’s Logo, Cabri and Excel, but also with other creative and expressive software. He has used these, not only as a fun and meaningful approach to many mathematical topics in the official syllabus, but also to introduce more “advanced” mathematical concepts.

As we explained in Jiménez-Molotla & Sacristán (2010), in the academic year 2005-06, Jesús and Alessio began a technology-based approach for the learning of trigonometry: the “Painless Trigonometry” long-term school project. In the first two academic years (2005-2006 and 2006-2007), approximately 250, 12-14 yr-old students, in grades 1 and 2 in two schools, were introduced to the Pythagorean theorem, basic trigonometry concepts and functions, and their applications using explorations and constructive activities with Cabri, Excel and Logo. At Eurologo 2007, the results of that initial project were presented (Jiménez-Molotla et al., 2007).

Trigonometry is not a topic that is included in the curriculum for that school level and is traditionally difficult to teach and learn; we used technology-based activities and constructions to give early access to that topic and provide experiences and “powerful ideas” (Papert, 1980) that might develop useful intuitive ideas (diSessa, 2000) on which to build upon later. At the same time we could cover other mathematical topics included in the official curriculum, such as: addition, subtraction, multiplication and division; powers and square root of whole and rational numbers; algebra (including constants, variables and polynomials); and geometry.

When that first project began, we never imagined the journey it would lead us on, creating a foundation for further trigonometry-based projects, such as the “Looking for the fourth dimension” 2007-2008 project (see Jiménez-Molotla et al., 2009), which led us to incursion in 3D geometry and the construction of pyramids in Logo; and the “Eiffel tower project” in 2009-2010 (see Jiménez-Molotla & Sacristán, 2010), where students engaged in the computer construction of that monument, using trigonometric ideas, pyramids and prisms ,as building blocks. All of the final constructions were carried out with Logo, but several other tools are also used for analysing figures and mathematical ideas, including Dynamic Geometry, Google Sketchup and Excel.

We would like to comment here on the emphasis we place on Logo in our projects. We feel that every mathematics programme should have some programming (or, at the very least, constructionist) activities; in our case it has been with Logo. We have delved into trying out other programming tools such as Scratch, but we always return to Logo, despite, on occasions, being under pressure to drop it from representatives of the Ministry of Education, or other colleagues, who claim it is outdated. We rely on Logo because we have not found a better tool in terms of both accessibility and power, and, of course, underlying constructionist philosophy and potential. And its influence has made us develop more constructive activities with other tools. Moreover, as it is illustrated later in this paper, students greatly enjoy and appreciate working with Logo.

In fact, though Logo is a central tool for us, we also believe in the importance of using, in an integrated and complementary way, a variety of tools for learning, since we consider that each tool brings with it a different type of knowledge and constitutes a different epistemological domain (Balacheff & Sutherland, 1994), and in this way we can provide several approaches and modes of representation with which students can engage and interact, thus enriching their learning experience (Wilensky, 1991).  That is why other tools, such as Cabri, Spreadsheets and Google Sketchup, are always used according to a particular situation.

All of the projects described here are long-term projects lasting most of the academic year. This gives the opportunity to articulate the projects with the academic requirements of the official curriculum; the technology-based activities are interspersed with regular mathematics lessons and paper-and-pencil activities, but in a way that allows for all of the academic activities to be integrated. Moreover, working long-term on these projects allows students time to assimilate and explore the mathematical and technical ideas, as well as time to work on their computer constructions and the problem-solving and analysis that those constructions require.  However, it is worth noting that every year we work with different students, so there is no continuity from one project to the next; that is, though each project builds on ideas developed in previous ones, we start from scratch each year with new students.

The 2011-2012 projects

In the academic year 2010-2011, we had as aim for our students to construct a computer model of the Parthenon. As has happened every academic year, we began with new students, so these students had to become familiar with the computer tools, with programming, etc.; as well as with the pedagogical model – where they are in charge of, and collaborate on, the explorations and constructions, and where the teacher acts as a guide – (students are not accustomed to this). However, that year it took longer, so none of the students completed the construction of the Parthenon; only some 3D animations and partial Logo constructions were achieved.

Figure 1. Cover page of the Parthenon project’s blog	Figure 2. Resources on the blog: e.g. a link for downloading Logo and trigonometric table

This academic year, 2011-2012, there was an extra motivation to finish the constructions before the conference in Athens, so more time and effort was spent on the project. As has been done since the Paris project, a blog (Figure 1) was set up for structuring the project, for providing classroom resources (Figure 2) and as a place for students to upload and share their constructions and comments. As in all previous years, this project was carried out with all the groups in which Jesús teaches (several Junior Secondary Grade 1 and Grade 2 groups in two schools).

Groundwork: basic shapes, triangles, playing and animated 3D constructions

The activities began by learning to construct the basic shapes that would serve as foundations for later constructions. Dynamic geometry constructions with Cabri and Google Sketchup are used to create an understanding of the structural components and mathematical relationships, serving, as well, as a comparison and complement to the Logo productions, where the construction process and its relationships are carried out and expressed in very different ways. Spreadsheets are also used to organize the information and also to express the mathematical relationships. The interaction and complementarity of the constructions with the different software tools enriches the activity and understandings of the students and helps finish the project. It is worth noting that during each session, students are given some time to play with their constructions freely. Over the years we have found that students get more engaged with their constructions if they can play with them; it is an important motivating factor.

After the initial investigations with various software and basic programming activities with Logo, students are introduced to three dimensional work. Through this 3D work, students discover that geometrical bodies are constructed using basic geometric shapes, for example by rotating them (Figure 4). In order to work with 3D, we have found it invaluable to create a system of axis and cartesian planes to help with orientation; this work is thus an excellent way to introduce students in Grade 1 to negative and positive numbers, a topic from the curriculum that is normally presented in the month of February, but by doing this work, it can be presented several months earlier. Students also start trigonometric work: in Figure 4, students rotated a triangle that is constructed using the Pythagorean Theorem and the arctan function (see the corresponding MSWLogo procedure, which is the same one used in all the programs presented in this paper).

to triangle :x :y fd :x bk :x rt 90 fd :y lt 180 rt arctan :x/:y fd  sqrt(:x*:x  + :y*:y) rt 90 - arctan :x/:y  lt :x end

Figure 3. 3D construction using triangles, with Logo code

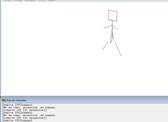
Figure 4. Animated rotating flag in 3D Logo	Figure 5. Animated car-wheels	Figure 6. Animated human figure

Part of the 3D work includes learning to animate: 3D figures cannot be fully appreciated if seen from only one angle. One of the animation tasks that we’ve found particularly useful is rotating a flag (Figure 4). This year students also animated car wheels (Figure 5) and a person (Figure 6).

Measuring the Earth using Eratosthenes’ method

Half-way through the academic year, we had the opportunity to participate in a project organized by the IFE-ENS Lyon, France, where a dozen school-groups from around the world measured the Earth’s circumference and radius using the method of Eratosthenes, and shared their results in a video-conference on 16 December 2011 (see http://artsandstars.ens-lyon.fr/ArtsAndStars/ eratosthenes/20111216/ index). This was a very convenient addition to our painless trigonometry activities, where the knowledge that had been developed through the previous tasks and Logo constructions could be put into use. Moreover, this was also an opportunity to get involved in a cross-disciplinary project where students could use mathematics in real-life situations. Thus, one of the geography teachers was invited to collaborate in order to help students understand what had to be taken into account in the measurements; he gave information on the meridians and the Tropic of Cancer in order to explain how our position on Earth is located at a tangent to the Earth’s radius. With this information, Google Sketchup was used to create an animation (Figure 7) of the Earth with its axes, meridians, etc.

Figure 7. Meridians and tropics of the Earth (left) & animated model using Google Sketchup (right)	Figure 8. Measuring the angle between the sun rays and the vertical direction  .	Figure 9. This team overlooked using the correct height for the pole.

Having had this insight, the next step was to use 1.5 meter-high poles as the tool (the gnomon) to measure, in the school courtyard (Figure 8), the length of the Sun´s shadow and determine the angle between the sunrays and the vertical direction (the solar zenith angle A) using the property that tan(A) = (length of shadow) / (height of gnomon). Teams of students were free to use any materials and carry out the measurements in the way they wanted; however, in one case, the task was so free that a team of students overlooked using the proper height for the pole (Figure 9).

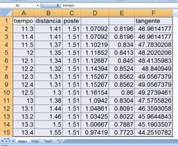
Figure 10. Collective record of the measurements.	Figure 11. Spreadsheet with collective measurements.

In December, 2011, ten days before the solstice, measurements were carried out every ten minutes, beginning at 11:10 in the morning, in order to determine the shortest shadow that would correspond to noon time. Each team recorded their measurement on the classroom’s whiteboard (Figure 10) and all the students could use the collective measurements, also recorded in a spreadsheet (Figure 11) in order to calculate the tangents. The school in Mexico City was partnered with a school in Chile (therefore each was positioned in a different meridian) so that using both schools’ measurements (the zenith angle found by each school), and the distance between the two positions, the Earth’s circumference could be calculated. Participating in this project was highly motivating for the students. The results of all the participating schools can be viewed at http://artsandstars.ens-lyon.fr/ArtsAndStars/eratosthenes/ 20111216/2011-dec-solstice.

Building the Parthenon model

The Eratosthenes project was a nice way to put into practice some of the trigonometry learned on the journey to build the Parthenon model. Having the trigonometric and other necessary foundations, and thanks to the incursion into 3D constructions, work on the Parthenon could begin. Over several sessions, several attempts were made: First with Cabri, but the work was tedious and after several sessions of incomplete work (Figure 12), the students abandoned it. Models with Google SketchUp were much easier (Figure 13) but it was collectively decided that with Logo it was more interesting. One of the initial approaches was to build a rectangular base with superimposed circles that would form the columns. In Figure 14 and the accompanying code (translated from the original Spanish), one of the first attempts at building the Parthenon in Logo is shown. The student in this example avoided variables, but used multiple turtles, so that different turtles drew each column. It is worthwhile noting that in the EMAT version of MSWLogo that is used, the primitive circle has been deactivated so that students are forced to reflect on how to create their own procedure for this shape.

Figure 12. The furthest attempt to model the Parthenon with Cabri	Figure 13. Modelling it with Google SketchUp	Figure 14. One of the first attempts towards modelling the Parthenon

to floor
setturtle 0
downpitch 90 rectangle downpitch -90
setturtle 1 downpitch 90 fd 100  downpitch -90
setturtle 2 downpitch 90 fd 100  rt 90 fd 200 downpitch -90
setturtle 3 downpitch 90 rt 90 fd 200   downpitch -90
end

to column0   <same code for: to column1, to column 2, to column3>
setturtle 0 <or correspondingly:  setturtle 1, setturtle 2,  setturtle 3>
downpitch  90
repeat 50[circle downpitch -90 fd 3  downpitch 90 circle]
end

to columns column0 column1 column2 column3 end	to frontis setturtle 4 fd 150 rightroll 90 rt 30 triangle end
to rectangle setturtle 0 repeat 2[fd 100 rt 360/4 fd 200 rt 360/4] end		to circle repeat 360 [fd .3 rt 1] end

A following step was to build the roof (Figure 15), something that required trigonometry. It was also collectively decided that the best approach for the base of the Parthenon was to have a rectangular prism (instead of simply a rectangle) – see Figure 16. Below we show the Logo code created by a student, Carlos, for his Parthenon model (Figure 17).

Figure 15. Roof of the Parthenon	Figure 16. Base of the Parthenon	Figure 17. Carlos’s model of the Parthenon

 

to partenon base setpencolor 20 fd 10 rt 90 fd 10 lt 90 downpitch -90 repeat 17 [ column1 downpitch 90 rt 90 penup fd 35.3 lt 90 downpitch -90] downpitch 90 lt 90 fd 10 rt 90 fd 390 lt 90 fd 600 lt 90 fd 20 lt 90 fd 10 lt 90 downpitch -90 repeat 17 [ column1 downpitch 90 rt 90 penup fd 35.3 lt 90 downpitch -90] setturtle 1 penup setpencolor 2 lt 90 fd 300 rt 90 fd 20 downpitch 90 fd 10 rt 90 fd 10 lt 90

repeat 6 [penup fd 50 pendown downpitch -90 column1 downpitch 90] setturtle 2 penup rt 90 fd 300 lt 90 fd 20 downpitch 90 fd 10 lt 90 fd 22 rt 90 repeat 6 [penup fd 50 pendown downpitch -90 column1 downpitch 90] setturtle 4 lt 90 fd 300 rt 90 fd 20 penup fd 150 pendown base0 setturtle 3 setpencolor 10 penup lt 90 fd 300 rt 90 fd 20 fd 150 downpitch 90 fd 200 rt 90 downpitch -90 fd 10 roofcover end

to column1 repeat 50 [downpitch 90 circle 1 5 downpitch -90 penup fd 3 pendown] repeat 50 [downpitch 90 circle0 1 5 downpitch -90 penup bk 3 pendown] end to base0 setpencolor 0 repeat 16 [downpitch 90 square 400 600 downpitch -90 fd 1] end

to circle :x :y repeat 360 [fd :x rt :y] end to circle0 :x :y repeat 360 [bk :x lt :y] end to square :x :y repeat 4 [fd :x rt 90] end to roofcover repeat 87 [roof downpitch 90 penup fd 7 downpitch -90 pendown] end

 

to base setpencolor 0 downpitch 90 rt 90 penup bk 300 lt 90 pendown repeat 20 [square 400 600 downpitch -90 fd 1 downpitch 90] setpencolor 0 repeat 55 [fd 6 rt 90 fd 600 lt 90 fd 1 lt 90 fd 600 rt 90] penup bk 400 fd 18 pendown end

to roof triangle 100 200 triangle 100 150 triangle 100 100 triangle 100 50 rightroll 180 triangle 100 200 triangle 100 150 triangle 100 100 triangle 100 50 rightroll 180 end

An important point here is that these constructions were built by the students themselves through a collaborative process over several months. Regardless of the approach, what matters is that the students achieved the goal. Here are some comments (translated from the original Spanish) that Carlos and other students made and posted on the project’s blog:

Carlos: this was a great experience that motivated me …. It was a bit difficult, but I think we had a good result and I am very excited that it may get sent to Greece.

Ocaltzin: the Parthenon was a difficult challenge but very fulfilling, because to be able to build that marvel with a single program was so fulfilling. The most difficult part was when some instructions didn’t come out as expected, then I had to look for what was the problem and fix it. But what drove me was to share this internationally, and that it would be something that would help me in the future. I liked very much how, through the [Logo] instructions given, it was a way to go over mathematics.

Emiliano: this Greek project was very interesting. Through Logo, we create the Parthenon using different formulas. I am very impressed with [its] value. Many schools in Mexico don’t have Logo but we do… this project is very important … we [need to] take advantage of this opportunity because next year we may not have it… our teacher is the only one that does these things and uses [Logo] in our school. This project sometimes was difficult and most of the time not easy, but it’s been fun and interesting.

Paulina:  we have learned a lot about mathematics with Logo and the Greek Parthenon project was a bit complicated but in the end we could do it. I believe that this has been a great teaching that we have learned through the project, putting into practice our mathematical knowledge and creativity.

Eric: The Greek Parthenon project was a challenge, but for me Logo will help me in my career because I want to study to be a programmer.

Itzel: This project was very good, a bit hard but possible to achieve. It was a great experience to construct the Parthenon in Logo. I hope it gets accepted (:

Martin: Logo is a great software, very interesting. I’ve learned to do many things. I had trouble with many things and often I made mistakes before finishing, but as we progressed I liked it more and more and also got better. This has really been a challenge and its been an effort. I really appreciate learning this; it is the best software I’ve used…. Thank you!

Paola: I had learned Logo before [in primary school] but not well. Now … I’ve learned to use it and I like that … it is very interesting to do something interesting and exciting and every day something different. Logo helps do many things and can help [in the future] and is motivating for doing new things… The Greek project is very interesting, and also fun, that helps to know more things.

Andrea: What I’ve liked is that through Logo I am learning programming and I like that very much because it may help me with when I do my career, and also for works and projects in my school. And I think the Greek project is a homage to Greece and very important for Mexico.

Fany: Teacher, I want to tell you that I admire… how you make us understand, and how you work. I finally understand mathematics more or less. Thank you!

As we can see from all these transcripts, students agree that the project was a challenge and sometimes quite difficult, but they enjoyed this and are grateful. We also see how much they appreciate Logo. When students program through Logo, the graphic constructions are a result of doing mathematics: the construction of the Parthenon was a learning result in which mathematics were lived in a new way with hits and misses. As their interest in mathematics was awakened, it was also observed that their understanding of regular mathematical school work improved.

Challenges

Despite continuous reforms, there are little real changes in education in our country. Projects like the ones carried out by Jesús are much more appreciated abroad than in Mexico; similarly with programs based on constructionist or constructionism philosophies, such as the EMAT program, which (though appreciated locally) are no longer supported by the Federal government whose current focus is for developing competencies in the use of office software suites.

Jesús feels that Logo, in particular, is a means for uncovering the genius in children, some of who sometimes do not do so well in traditional school settings. This was the case of one boy who excelled in the “In search for the fourth dimension” painless trigonometry project that focused on the construction of 3D pyramids (Jiménez-Molotla et al., 2009): This student won several academic competitions, including one with the work done in our project, against university students who had won international contests in robotics; he even won a spelling contest; yet the school expelled him because he was too restless and they didn’t know how to handle with him.

Also during the Eratosthenes’ method tasks, some colleagues questioned why “waste time” on this; Jesús had to respond, using Asimov’s (1972) words, that it is important for students to rediscover what has already been discovered. The Eurologo/Constructionism community has been an inspiration to continue the search on how to bring light and a new identity to education in our country.

Expansion of the projects, further research and concluding remark

All of the past projects in which we have been involved, have opened the possibility to expand further. A few years ago, Jesús could not believe that activities like these could be done with younger students; however, he has now been invited to collaborate with a small primary school, the Liceo “Robert Owen”, in a village outside Mexico City. This is a school for which Jesús, who is an architect (besides being a mathematics teacher), had designed the building over 15 years ago (and he had done so in the shape of a castle with a tower “so that children can go up, be close to their dreams and be inspired”). Jesús had never had any experience with primary schools. But he is inspired by Richard Noss who once told him that “knowledge has no age; it is all about how it is taught”. So he is now collaborating with the last two grades of that primary school, with some in-presence sessions, online and via video conferences. In his initial presentation to the school he told them that they would be like warriors defending Ancient Greece, inspired and motivated by the land of Pythagoras and Eratosthenes. The school, principal, teachers and children are so far highly motivated and excited about this incursion into digital technologies and Logo.

This is the kind of motivation that the Eurologo/Constructionism conferences have brought. In this case, the host city for this year’s conference, not only inspired the Parthenon project described above, but has also inspired the way in which Jesús is now incursioning into primary schools, incorporating digital technologies in a way that is not just about using those technologies or perhaps new software that is in fashion, but rather as a means to construct meaningful learning. Because projects like the Parthenon one are not just about drawing a model, but rather are constructionist approaches.

On a separate note, we are now in the process of researching the long term impact of the participation of students in these projects. This has been challenging as it is difficult to track down students who have moved on to high-school and therefore are no longer readily available since the schools were we work do not go past Grade 3 (students aged 14-15) of middle-school. However, we have located a few of them and are interviewing them. We are interested in seeing how one school-year in the life of these students, of whom many claim, as seen in the transcripts above, that these experience would help in their future careers, has actually influenced their future learning and life.

It has been ten years in which Jesús and I have worked together. In those ten years we have seen the evolutions of these painless trigonometry projects and this year it was very fulfilling to be able to put to practice some of the trigonometry concepts developed in the projects for the measurement of the Earth. We look forward to further projects in this and other directions.

Acknowledgements

We acknowledge the collaboration and help in the design and implementation of these projects of Alessio Gutiérrez-Gómez of the Secundaria #229 “Ludmila Yivkova” in Mexico City. We are also grateful to all the children and schools with whom, and in which, we have worked: Secundarias #229 “L. Yivkova” T. Matutino & #139 “J. E. Rodo” T. Vespertino; Liceo “Robert Owen”. Jesús would also like to thank the members of the Eurologo/Constructionism communities who inspire him to continue, including Richard Noss, Celia Hoyles, Ivan Kalaš, and of course Seymour Papert and Wallace Feurzig, among many, many others.

References

Asimov, I. (1972). The Left Hand of the Electron. New York: Doubleday.

Balacheff, N. and Sutherland, R. (1994) Epistemological Domain of Validity of Microworlds: The Case of Logo and Cabri-géomètre. In R. Lewis & P. Mendelsohn (eds) Lessons from Learning, IFIP Conference TC3WG3.3, North Holland, pp. 137-150.

diSessa, A. A. (1997). Open toolsets: New ends and new means in learning mathematics and science with computers. In E. Pehkonen (ed.), Proceedings of PME 21, Vol. 1, pp. 47-62. Lahti, Finland.

diSessa, A. A. (2000). Changing minds: Computers, learning, and literacy. Cambridge: MIT Press.

Harel, I., & Papert, S. (eds) (1991). Constructionism. Norwood, NJ: Ablex Publishing Corporation.

Jiménez-Molotla, J., Gutiérrez-Gómez, A., & Sacristán, A. I. (2007). Painless Trigonometry: A Tool-complementary School Mathematics Project. In I. Kalaš (Ed.), Proceedings of the 11th EuroLogo Conference: 40 Years of Influence on Education (pp. 1-11). Bratislava, Slovakia: Comenius University.

Jiménez-Molotla, J.; Gutiérrez-Gómez, A., Sacristán, A.I. (2009). Pyramids in Logo: A School Project in ‘Search’ of the Fourth Dimension. In A. Tatnall & A. Jones (Eds.) Education and Technology for a Better World (pp. 92-101). Boston: Springer.

Jiménez-M., J. & Sacristán, A.I. (2010). Eight years of journey with Logo leading to the Eiffel tower mathematical project. In J. Clayson & I. Kalas (Eds) Constructionist approaches to creative learning, thinking and education: Lessons for the 21 st century – Proceedings Constructionism 2010 (12th EuroLogo conference), AUP / Comenius University.

Papert, S. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.

Wilensky, U. (1991). Abstract Meditations on the Concrete, and Concrete Implications for Mathematics Education. In I. Harel & S. Papert (Eds) Constructionism (pp. 193-204). Norwood, NJ: Ablex