A Constructionist Method for Teaching
Teachers about Basic Properties of Complex Systems, using a NetLogo Model.
Gkiolmas Aristotelis, agkiolm@primedu.uoa.gr
Department of Primary Education,
University of Athens, Greece
Chalkidis Anthimos, achalkid@gmail.com
Department of Primary Education,
University of Athens, Greece
Karamanos Kostas, koskaraman@gmail.com
Department of Primary Education,
University of Athens, Greece
Papaconstantinou Maria, mpapakonstan@hotmail.com
Department of Informatics, Ionian
University, Corfu, Greece
Skordoulis Constantine, kostas4skordoulis@gmail.com
Department of Primary Education,
University of Athens, Greece
Abstract
The current research report discusses a
Constructionist approach used to teach prospective Greek Primary School
Teachers, about five certain properties of Complex Systems (CS’s), by the use
of the programming and modeling environment of NetLogo, and especially by the
use of a NetLogo Model called “Ants”. The research presented here was part of a
broader research project, which had as central research question: if and
to what extend the NetLogo models can help future educators conceptualize
specific properties of Complex Systems in nature. Students underwent approximately
one-hour-lasting interviews, by the first of the authors, which were fully
recorded. The whole interview was taking place in front of a computer, which
had the NetLogo Model “Ants” activated, as well as some variations of it,
created by the researchers. The students interacted with the model all of the
time, in a constructionist manner of learning and discussing, and in an
inquiry-based-learning strategy, so as to complete the interview.
After the thorough examination of the
results obtained by the interviews, it becomes evident that: the use of the
NetLogo Model helps undergraduate Primary School Teachers conceptualize five
basic properties of the Complex (Adaptive) Systems, and to build a
representation of the comportment of these systems on their own.
Keywords
NetLogo, undergraduate teachers, teaching,
complex systems.
Introduction.
The core idea
behind constructionist teaching, which is learning-by-making (Papert and Harel,
1991, Papert, 1980), as well as working with the learner with a not-so-much
predetermined plan, but changing the teaching methodology according to the
feedback that the teacher receives in each step of the teaching sequence, is
optimally applied by the use of computers. (Kafai & Resnick, 1996). The use
of the Logo-like environments is appropriate for involving the learner in
activities which would lead him, with the instructor only as a mediator, to the
cognitive results aimed at, as much of the literature proves (Healy &
Hoyles, 2001; Laborde et al., 2006). An environment used extensively in the
recent years for teaching learners of various ages about basic concepts of
Mathematics and Science, is NetLogo (Wilensky, 1999). NetLogo is a
Multi-Agent-Based Modeling and Programming environment based in the Logo
language as invented by Seymour Papert, and to the StarLogo Microworlds as
invented by Mitchel Resnick. The use of many “turtles” (agents), the number of
which is determined by the user, as well as the user-friendly interface makes
NetLogo an ideal tool for instruction, especially for the conceptualization of
complex systems (Tisue & Wilensky, 2004). A lot of research has been
carried out on what exactly “conceptualization of complex systems means”
(Jacobson, 2001) and more specifically what shift in the person’s way of
thinking this requires, and to what aspects of the system’s conceptualization
it refers, such as the Structure, Behavior and Function (SBF) (Hmelo-Silver
& Pfeffer, 2004). Especially researchers like Sharona Levy have extensively
used the programming environment of NetLogo in empirical researches to see how
it affects the learners’ understanding of Nature (Levy & Wilensky, 2008;
Levy & Wilensky, 2011). In this research, the model “Ants” from the NetLogo
Models’ Library was chosen, since it addresses a natural-like system that is
both complex and adaptive, like many other natural systems
(Levin, 1998). In addition to this, the Model “Ants” – which also exists in
StarLogo (Resnick, 1997) – helps the learning subject develop certain mental
qualities. Such qualities are: (i) decentralized thinking (Resnick, 1996;
1998), which means understanding that a system may work without a central
control or leader and (ii) thinking in levels (Wilensky & Resnick, 1999),
which means realizing that local interactions among members of a system may lead
to a totally different and unexpected overall behavior.
The research
presented here was part of a broader research project, which had as its central
research question: “if and to what extend the NetLogo models can help
future educators to conceptualize specific properties of Complex Systems in
Nature”. These properties included the ones discussed in this paper,
which are: (i) self-organization, (ii) lack of central control or leadership,
(iii) emergence of an overall (human-intelligence-like) behavior through local
exchange of a simple set of information, (iv) non-repeatability, even with
identical initial conditions (stochastic properties) and (v) existence of
critical values for certain parameters.
The Sample and the Research Procedure.
The research
was addressed to undergraduate students of the Department of Primary Education,
University of Athens Greece, who had chosen to be taught the optional course:
“Environmental Science and Education: The Laboratory Approach”. The
Constructionist context of introducing students to Complex Systems (and mainly
ecosystems as Complex Systems), consisted in having them in pairs in front of
Computers in which the NetLogo Models were installed, and having them trying to
find out what the model (here “Ants”) does and how they can interact with it.
The answers were written on worksheets. This constructionist introduction to
the NetLogo Model is explained in APPENDIX .
After the
familiarization with the NetLogo environment and with this specific model, the interview
with each pair of students followed.
Each interview,
during the research process, was aimed at referring to one couple (n=2) of undergraduate
students (when it could not be achieved, instead of two, one was interviewed).
It lasted one hour to one hour and a half.
The couple
started by being acquainted with the NetLogo Model, the specific one being
“Ants”, by playing with the buttons and the sliders and by watching the screen.
Simple initial questions accompanied this procedure such as: “what do you think
this button/slider does?” or “what is this that you watch in the screen?” or
“what do you notice?” The main questions of the interview had always three
phases: (a). Answer before you try it in the model (prediction), (b). Answer
after you try the model many times and – if you like – change the parameters
(testing) and (c). Compare (a) and (b) and reach a final answer. Also give your
explanation why your answer is valid.
Each one of the
two students in the couple (when in couples) could discuss with the other in
stages (b) and (c).
The specific sample which participated in the interviews
were N=15 undergraduate students of the Department of Primary Education of the University of Athens. This sample was part of a larger research sample, consisting of 85
students, who participated in the overall research. All of these 15 students
were attributed with specific values for four different parameters, i.e.:
§ Year of Study. The parameter takes the values: A, B, C and D (no students of the
Department of later years participated).
§ Orientation during the Third (final) Class of
High-School. The parameter takes three values: Sc (Science) – did not exist in this specific sample – Theor (Theoretical,
Classical Studies) and Tech (Technological).
§ Whether or not they had chosen Biology as an
exam topic for the entry exams to the University.
The parameter takes two values: Biol-YES (Y) and Biol-NO (N).
§ Whether or not they had chosen Informatics
among the optional topics either in the years of the high-school or in the
University. This parameter takes two values: Info-YES (Y) and info-NO (N).
In the Table 1, which follows, the values of the
parameters for each member of the sample that was interviewed are provided.
Student’s Number |
Year of studies |
Orientation |
Biology |
Informatics |
1 |
3 |
Tech |
N |
Y |
2 |
3 |
Theor |
N.A.S |
N.A.S |
3 |
4 |
Tech |
N.A.S. |
N.A.S |
4 |
3 |
Theor |
N |
Y |
5 |
3 |
Theor |
N.A.S |
N.A.S |
6 |
3 |
Theor |
Y |
N |
7 |
3 |
Theor |
Y |
Y |
8 |
3 |
Tech |
Y |
Y |
9 |
3 |
Theor |
N.A.S |
N.A.S |
10 |
2 |
Theor |
Y |
Y |
11 |
2 |
Theor |
N.A.S. |
Y |
12 |
2 |
Tech |
N |
Y |
13 |
2 |
Theor |
N |
Y |
14 |
3 |
Theor |
Y |
Y |
15 |
3 |
Theor |
Y |
Y |
Table 1. The sample
interviewed, with respect to the values of the parameters.
Each pair of students were initially interviewed with
respect to the initial “Ants” Model of NetLogo (Wilensky, 1997), with the
slight difference that the sliders, the buttons and the rest of the NetLogo
interface screen was translated in Greek. This is shown in Figure 1, below.

Figure 1. A
screenshot of the NetLogo Model “Ants”
At a later stage of the interview, the undergraduate
students were asked questions about a variation of the Model “Ants”, in which
there are only two food-sources, identical and equidistant from
the ants’ nest. In Figure 2 below, a screenshot of this Model is given.

Figure 2. A screenshot of the NetLogo Model “Ants” with ONLY TWO food piles, in EQUAL DISTANCES from the
nest.
Finally in the interview, a variation of the Model
“Ants” is used, in which there is only one food-source, but with an
obstacle between the ants’ nest and the food source. In Figure 3 below, a
screenshot of this Model is given.

Figure 3. A screenshot of the NetLogo Model “Ants” with ONLY ONE food pile, and AN OBSTACLE between the ants’ nest and the
pile.
The interviews with
the students were conducted in front of a PC screen, with the NetLogo models
installed on it, by the first of the authors, and were built within a
constructionist framework, combined with inquiry-based-learning techniques.
Simultaneously
to this sample, a control group was formed with NCONTR = 8 untergraduate students. They were also divided in four pairs, they
had a similar distribution of parameters with the one given in Table 1, and
they gave identical interviews with the initial sample, with one major
difference: they did not have a computer and did not interact with the NetLogo
Model at all. Instead, the model “Ants” was described and taught to them on
whiteboard, step-by-step, by the first of the authors.
Results and Discussion
A. Initial “Ants” Model of NetLogo.
As becomes
apparent from the interviews, the students (Question 2, “Which is the inherent logic of the accumulation of food within the
population of the ants?”) tend to see a centralized
control for the ants’ troop, as they initially become acquainted with the
model. Out of the N = 15 students,
§ the N1= 0, before their
further involvement with the model, tend to believe that the first ant that
reaches the food-pile, is some kind of leader for the others.
§ the N2 = 14 give
scientifically “wrong” answers about the role that the pheromone plays (the
“white” substance).
§ the N3 = 5 have not a clear
image of the role that the number, (the “population”) of the ants plays
in the time-evolution of the model.
§ the N4 = 5 are not able to
determine what is the effect of the value of the sliders: “diffusion-rate” and
“evaporation-rate” to the consumption of the food piles.
§ the N5 = 2 seem to believe
that the order by which the food piles are consumed will always be the same,
no matter how many times the model’s run is repeated.
§ the N6 = 14 argue (in various
ways) that the fact that the first food pile eaten is the closest to the nest,
is statistically explained, i.e. more ants “hit” it, due to proximity.
In the control group, the corresponding numbers were:
NCONTR,1 = 6, NCONTR,2 = 6, NCONTR,3 = 6
NCONTR,4 = 8, NCONTR,5 = 6, NCONTR,6 = 8
But as the constructionist interview proceeded, and they
played several times with the model, the numbers clearly improved:
§ N1
remained N1΄ = 0
§ Ν2 was reduced to Ν2΄ = 2
§ N3 was
reduced to Ν3΄= 0
§ N4 was
reduced to Ν4΄= 0
§ N5 was
reduced to Ν5΄ = 1
§ N6 was reduced to Ν6΄ = 1.
The results are graphically shown below
(fig.4):
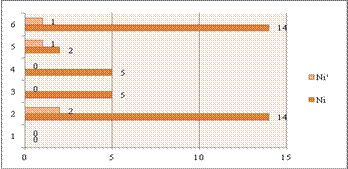
Figure 4. The “answers” before (Nx) and after (N’x) the interview (Model
“Ants”)
The corresponding results in the control group were :
N΄CONTR,1 = 5, N΄CONTR,2 = 5, N΄CONTR,3 = 6
N΄CONTR,4 = 6, N΄CONTR,5 = 6, N΄CONTR,6 =
8
Other results stemming from this initial application of
the Model “Ants” in the interviews were:
§ The Ν5=2
students belonged to the same group, when the research was carried out in the
overall sample.
§ The members of
the sample who had taken Biology as an optional topic
(NBIOL = 6 in total) for the University Entrance exams, gave more well-documented and combinational answers,
as regards the parameters of the pheromone (diffusion rate and evaporation
rate).
§ The persons that
had entered University in another way (those taking older forms of entrance
exams, those moving to the Education Department after completing studies in
another Department or people from Cyprus) gave very simplified answers.
B. Variation of the “Ants” Model, with
two equidistant food-piles.
In the beginning,
out of the N = 15 undergraduate students, only N7 = 2 realized that one
of the two food piles will clearly be consumed first. The others thought that
they are consumed practically simultaneously, with a slight advance of one of
the two.
Also, N8 = 5 believed that the pile consumed first is always the same one,
or at least in most cases.
In the control
group, the corresponding numbers were:
NCONTR,7 = 4, NCONTR,8 = 6.
Later, after extensive trials of the model, the numbers
improved.
§ N7 increases to N7΄ = 6
§ Ν8 falls dramatically to
N8΄ = 0
The results are
graphically shown below (fig.5):
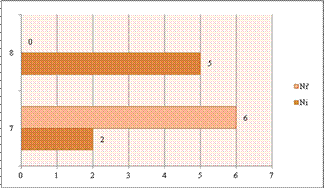
Figure 5. The “answers” before (Nx) and after (N’x) the interview (Model
“Ants, variation with two food-piles”)
The corresponding results in the control
group were :
N΄CONTR,7 = 5,
N΄CONTR,8 = 6.
Further analyzing the interviews’ results, it could be
seen that:
§ The Ν7 = 2
considered both food piles as equally capable of being consumed first, still
only one of them, they said, will precede.
§ As is
obvious both from numbers N7 and N7΄, the
prevailing view were always that the two equidistant food-piles would be
consumed practically simultaneously.
§ Once
more, the members of the sample who had taken Biology as an optional topic
(NBIOL = 6 in total) for the University Entrance exams, gave more
alternatives in their answers.
C. Variation of the “Ants” Model, with
one food-pile and an obstacle.
In the
beginning, N9 = 3 argued that the ants will bypass the obstacle in random ways.
Also N10 = 1 argued that they will create a
curved trajectory in the one side of the obstacle.
Only N11 = 2 could see that this curve will be
the tangent to the obstacle.
And only N12 = 4 were able to see that there will
be TWO such identical trajectories one adjoined the obstacle.
In the control
group, the corresponding numbers were:
NCONTR,9 = 5, NCONTR,10 = 2, NCONTR,11 = 4,
NCONTR,12 = 2
Afterwards, the Numbers get much better.
§ N9
reduces to N9΄ = 0
§ N10
reduces to N10΄ = 0
§ N11
increases to N11΄ = 12
§ N12 increases to N12΄ = 8
The results are graphically shown below
(fig.6):

Figure 6. The “answers” before (Nx) and after (N’x) the interview (Model
“Ants, variation with one food-pile and an obstacle”)
The corresponding results in the control group were :
N΄CONTR,9 = 2, N΄CONTR,10 = 2,
N΄CONTR,11 = 6,
N΄CONTR,12 = 4.
§ In
this latter form of the “Ants” Model, used in the interview process, the
students answered mainly based on their experience with NetLogo and on the
things they saw with the Models, regardless of their pre-existing knowledge.
§ In
this part, a great variety of answers were given, combining arguments in many
ways.
§ Again
in this part, the persons that had entered University in another way (those
taking older forms of entrance exams, those moving to the Education Department
after completing studies in another Department or people from Cyprus), found it
difficult to answer in many cases.
§ The vast
majority of the students coming from a theoretical orientation in high-school
(9 out of NTHEOR = 11), needed a lot of guidance
to formulate an answer.
Conclusions
Initially there
are some “case-affected” or technical conclusions from this research: At first,
the students coming from a technological orientation in high-school (NTECH =
4), did not encounter any special problem in handling the NetLogo interface, as
regards its usage and the understanding of its functions. Secondly, all of the
students of the sample (15 out of 15) altered their answers after testing the
Models many times, emphasizing on the usefulness of the method. Thirdly, most
of the inadequate answers came from the undergraduate students that had entered
University with another system of entrance exams, than the one mainly valid in Greece nowadays.
But stress
should definitely be given to the more general conclusions, referring to the
usefulness and the effectiveness of NetLogo, and this specific model, in the
conceptualization of Complex Systems on behalf of future educators.
First of all the
11 out of the 15 students – a percentage of around 73% – towards the end of
the interviews had switched to an almost common form of terminology, the one
appropriate for Complex Systems and for NetLogo, and they ended up giving
well-documented answers.
It should be
stressed also that when the undergraduate students were in couples, the answers
tended to be much more alike, since the discussion among them affected their
views. So we have a definite peer-effect very common in
constructionist methods working in pairs. The same is valid for the four groups
of the control group.
As can be seen
from the relatively poor performance of the control group, related to the basic
sample, NetLogo seems to be a great instruction tool for getting the learning
subjects acquainted with the properties of Complex Systems, compared to
classical, oral instruction. Complex systems are much better realized when
seeing them evolving in time on a screen, and when interacting with their
properties, than when being simply taught about them in a series of lectures.
Constructionist approaches and teaching
through NetLogo seems to be giving the learners, a better feeling about
understanding the subject of Complex Systems, compared to oral instruction. One
of the very last questions on the worksheet was: “Was it helpful, in
understanding?” and 11 out of the 15 students of the main sample answered
positively, as shown in the figure 7, whereas only 2 out of the 8
persons in the control group gave affirmative answer to this.

Figure 7. Answers in question: “Was it helpful,
in understanding?”
References.
Dresner, M. (2008). Using research projects
and qualitative conceptual modeling to increase novice scientists’
understanding of ecological complexity. Ecological
Complexity, 5(3), 216–221.
Gobert, J.,
D., O’Dwyer,
L., Horwitz P., Buckley B.
C., Levy S.T.
& Wilensky U. (2011). Examining the Relationship Between Students’
Understanding of the Nature of Models and Conceptual Learning in Biology,
Physics, and Chemistry. International Journal of Science Education. 33(5), 653-684.
Goldstone,
R., L., Wilensky,
U. (2008). Promoting Transfer by Grounding Complex Systems Principles. Journal
of the Learning Sciences, 17(4), 465-516.
Healy, L.,
& Hoyles, C. (2001). Software Tools for Geometrical Problem-Solving. International
Journal of Computers for Mathematical Learning, 6(3), 235-256.
Hmelo-Silver, C., E., & Pfeffer, M., G. (2004).
Comparing expert and novice understanding of a complex system from the
perspective of structures, behaviors, and functions. Cognitive Science,28, 127–138.
Jacobson, M. J.
(2001). Problem solving, cognition, and complex systems: Differences between
experts and novices. Complexity, 6(2), 1–9.
Jacobson, M.,
J. & Wilensky, U. (2006). Complex Systems in Education: Scientific and
Educational Importance and Implications for the Learning Sciences. The
Journal of the Learning Sciences,15(1), 11–34.
Kafai, Y.,
& Resnick., M. (1996) (Eds.). Constructionism in practice: Designing,
thinking and learning in a digital world. Mahwah, NJ: Lawrence Erlbaum.
Laborde, C.,
Kynigos, C., Hollebrands K., Strässer R. (2006).Teaching and Learning
Geometry with Technology. In A. Gutiérrez, P. Boero (Eds.), Handbook
of Research on the Psychology of Mathematics Education: Past, Present and
Future. pp. 275-304. Rotterdam: Sense Publishers.
Levin, S., A.
(1998). Ecosystems and the Biosphere as Complex Adaptive Systems. Ecosystems, 1 (5),
Levy, S.,
T., & Wilensky,
U.(2008). Inventing a “Mid Level” to Make Ends Meet: Reasoning between the
Levels of Complexity. Cognition and Instruction,
26(1), 1-47.
Levy, S., T., & Wilensky, U. (2011). Mining
students’ inquiry actions for understanding of complex systems. Computers & Education, 56, 556–573.
Papert, S.
(1980). Mindstorms: Children, computers, and powerful ideas. New York: Basic Books.
Papert, S.
& Harel., S. (1991). Situating Constructionism. In S. Papert & I.Harel (Eds.), Constructionism (pp. 1–11). Norwood, NJ: Ablex Publishing Corporation.
Resnick, M.
(1996). Beyond the centralized mindset. Journal of
the Learning Sciences, 5, 1–22.
Resnick, M. (1997). Turtles, termites, and traffic
jams: Explorations in massively parallel microworlds.Complex Adaptive Systems series. Cambridge, MA: MIT Press.
Resnick, M., &
Wilensky, U. (1998). Diving into complexity: Developin probabilistic
decentralized thinking through roleplaying activities. Journal of the
Learning Sciences, 7,
153–171.
Tisue, S.,
& Wilensky, U. (2004). NetLogo: A Simple Environment for Modeling Complexity. Proceedings of the International Conference on Complex Systems, Boston, May 16–21, 2004.
Wilensky, U. (1997). NetLogo Ants Model. http://ccl.northwestern.edu/netlogo/models/Ants.
Center for Connected Learning and Computer-Based Modeling, Northwestern
University, Evanston, IL.
Wilensky, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling,
Northwestern University. Evanston, IL.
Wilensky, U., & Resnick., M. (1999).
Thinking in Levels: A Dynamic Systems Approach to Making Sense of the World. Journal of Science Education and
Technology, 8(1) .
APPENDIX
The Constructionist set of Questions on the Worksheet, to introduce
students to NetLogo Model Ants.
1. What are the buttons that you see on this screen?
What do you thing each one is doing? (Always write your answers, after
discussing within the pair).
2. Try to press button named “SetUp” once. What is this
that you see in front of you?
3. Press “Go”. Can you find out what this troop of ants
does? Describe in your own words.
4. What is this white substance doing? Try to give a
description, after trying the situation many times (always restart by pressing
SetUp and then Go)
5. Do you see any resemblance with real ants? Give a
description, after trying the model as many times as you like, altering the
parameters.
6. What is shown on the plot, when you have it “on”?
7. What is the overall logic, or strategy, in the ants
motion? Can you see it?
8. What do you thing of the buttons “diffusion-rate”
and “evaporation-rate”? Try them with many different values to see if you can
find out what they are doing.
9. If you work with one ant, and then with very few
ants, do you notice any differences? Which ones.
10. In general, do you
see if the population of ants plays a role in the situation? If yes, how you
would describe it?

