The necessity of the tangent
Marios Spathis, mspathis@sch.gr
High School Teacher (K-12 Education), MSc, MEd
Eirini Kouletsi, kouleir@gmail.com
High School Teacher (K-12 Education), Med
Abstract
In this paper we present a didactic
proposal for a scenario in teaching trigonometric numbers and particularly the
tangent, designed for grade 8 students. The scenario is based on the theoretical
framework of constructionism. Looking back in the history of mathematics to use
those elements that led to the discovery of the concept we want to teach, we
create a problem-based learning environment supported by the E-Slate software,
from which we use the Turtleworld microworld. Students are engaged in a process
where they have to think a way which will allow them to construct scaffolds of
different lengths, but with the same slope, which will serve to build all the
levels, one by one, of a pyramid.
Keywords
Pyramid, scaffold, ladder, slope,
tangent, angle, constructionism
Introduction
Focusing on the constructivist ideas of Piaget and their expansion, due to Papert’s theory about constructionism, one can realise the huge
change that they bring to instruction and the designing of teaching. Knowledge
is structured not only with the individual’s experience, but especially with
his active involvement in its construction, using experimentation methods,
modelling and participatory notification of new cognitive acquisitions. As
referred to by Kafai & Resnick, (1996) it is the actual process of learning and teaching that is
compatible with constructionism.
In Mindstorms, back in
1980, Papert advocated “the construction of
educationally powerful computational environments that will provide
alternatives to traditional classrooms and traditional instruction.” The same time he noted technology of that time
was limited regarding its capabilities and ease of use. Since then, considerable work has been done ranging from Logo, Mindstorms,
Scratch, ToonTalk etc., that incorporate a constructionist approach to
learning (Girvan, C., Tangney, B. and Savage, T., 2010).
Several studies have focused on the
implementation of tools as a means of mediation to provide strong visual
intuitions supporting production of algebraic meanings and bridging the gap
between the act and expression.
The History of Mathematics, on the other
hand, provides a significant range of examples with which they can engage students
to build from scratch a notion, as when appeared for the first time the
necessity of its creation.
With the help of technology not only as a
tool but as well as an instrument and a mediator, on one and a historical event
related to the use of tangent in Ancient Egypt on the other, the students in
this paper will reconstruct the concept of tangent.
Theoretical Framework
As pointed out by E. Ackermann in a bibliographic article on the differences
between Piaget’s and Papert’s theories (2001), Psychologists and
pedagogues like Piaget, Papert but also Dewey, Freynet, Freire and others from
the open school movement can give us insights into: 1. How to rethink
education, 2-imagine new environments, and 3- put new tools, media, and technologies
at the service of the growing child. They remind us that learning, especially
today, is much less about acquiring information or submitting to other people’s
ideas or values, than it is about putting one’s own words to the world, or finding
one’s own voice, and exchanging our ideas with others.
Traditional teaching has received numerous criticisms for
its results. Contemporary teaching methods nowadays have left aside the
immediate information. It is in general accepted that students do not merely
take the information provided to them, but translate it according to their own
criteria based on their previous knowledge and experience. According to Piaget
students have serious grounds not to discard their views thanks
to an externally induced anxiety.
Also, the environment, as clearly studied and indicated by
Vygotsky, where the concept environment we mean all the characteristics of
local culture, such as language, instruments, people, plays its dominant role
in shaping the views.
Papert clarifies that constructionism —the N word as
opposed to the V word— shares the same views on learning, namely it must be “building knowledge structures” and this will be accomplished by progressive internalization of actions. This internalization is achieved by a
very cheerful way for the students, when done in a context that allows the
conscious engagement with a construction that can obtain public entity. He
extends Vygotsky’s views in contemporary situations, suggesting as mediation
tools the digital media and computers technology.
Our teaching proposal
A few words about the rationale of our
proposal
No one is to oppose that planning an
activity that motivates-engages students in experiments, computations and
assumptions with the aim to highlight a concept or a theorem only positive
results can bring, in general.
We estimate, in addition, if such an
engagement is based on the origins of the concept we want to teach, then more
active participation of the students is achieved. For such scenarios, when used
in the teaching of mathematics (as well as in physics), apart from the fact
that the students’s interest is raised, they also convey, without the need of a
modern translation, the ideas and knowledge that gave birth to them, since
they can approach them by experimenting, constructing and expressing in their
own way.
In terms of putting it in to action, we know
that Ancient Egyptians could estimate the slope of a line or a plane. In fact,
they used a ratio called skd (pronounced
seyket) that corresponds to our current contagent (Bunt, Jones, Bedient,
1981). We use this idea, with the appropriate didactical transformation, to
lead the students in a similar situation.
The approach followed
in our teaching is that of problem-based learning.
The implementation of the proposal
Our original scenario was designed to be
implemented on grade 8 school students in four (4) class hours. The first two
hours comprised the concept of the tangent angle as a necessary tool for the indirect
calculation of an angle, whereas the following two hours using that ratio to
calculate sides of a triangle similar to the original right triangle. Due to
space considerations in this paper we will present only the first two class
hours. The students work in groups of two or three in the computer lab, using
the E-slate software, on worksheets and workbooks.
We briefly present the problem to our students and which
substantially raises the following question: “While we have built the first row
of blocks of the pyramid and then by means of a scaffold build the second one,
where must we place the second scaffold to fill the third row? To what must we
pay attention?” This can be an initial discussion on the conditions and the
constraints we have in the construction, since the labors-workers will have to
work in the same conditions to perform the same, ie maintain the same slope in
all the scaffolds (or ladders as depicted on Figure1).
So, we have a figure as the following one, with the corresponding
reflection.

Figure
1. Where should the ladder be placed in order to construct the 3rd row?
Our aim is solely the discovery of the
tangent angle. For that, we focus on the first right triangle of figure 1 omitting the remaining elements of the problem and ask students to
construct this triangle. We proceed using the microworld Turtleworld of software
E-slate where we present a half –baked notation code to
the students, which is as follows:
to right_triangle :x :y :a
rt 90
fd :x
lt 180-:a
fd sqrt(power :x 2 + power :y 2)
lt 90+:a
rt :y
lt 180
end
And we ask to: 1. Interpret the notation code
2. To use the notation code to construct a right triangle of sides 40 and 30
turtle steps with an angle of 30 degrees. 3. Similarly, to construct a right
triangle of sides 160 and 120 turtle steps with an angle as the previous one. 4.
To activate the sliders of parameters (:x), (:y) and (:a), experiment and construct
the two triangles.
We ask our students to interpret the notation
code, to assure that all grasp it fully. Otherwise it is possible the
subsequent commands that will be asked to create just to play the role of an automation
button, slightly different to the ones used in their computer.
It is expected that some students will have
difficulty in perceiving mentally and describing the turn of the given angle in
the notation code. At this point we will explain to the students the reason why
we chose to deal with the given angle. We will need to draw a figure on the
blackboard, bring a parallel line from vertex C, to talk about corresponding
angles etc, as follows.
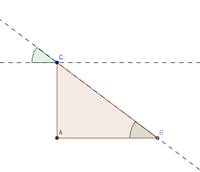
Figure 2. Corresponding
angles
We ask from our students to construct two
triangles, although they are meant to fail in both, for two reasons. The first
triangle is too small and it doesn’t provide a satisfactory visual effect,
whereas the second one will reveal the weakness of the construction. Also, the
sides of this triangle (the numbers corresponding to their length) in
combination with the former’s sides may give a first suspicion of ratios to the
students.
Some groups of students while experimenting
with the sliders of parameters (:x) , (:y) and (:a) -if not all- are expected to come up with an angle of 37ο that apparently leads to true results. At this point a software of dynamic
geometry would be useful, to easily construct the vertical sides of the
triangle and to realize, as much precision though they use, that the angle is
not 37ο.
Returning to microworld Turtleworld and our initial construction while we ask our students to construct a triangle
of sides 40 and 30 turtle steps we explain to them that the software has the
ability to calculate the angle precisely, if we give a numeric value as input to
the arctan ( ) command. (It would be useful to write that command in another
language different to the native language of the students, if there is such a
possibility from the program in order to minimize any kind of connotations that
can possibly appear). We encourage our students to experiment with the sides of
the triangle and the various relationships created between them.
The students will complete this phase by verifying
their conjectures for the construction of the second triangle and citing their
conclusions in the original problem of the construction of the pyramid.
As an epilogue
This proposal has not been implemented in
class, in order to be able to give some results. The idea of the design
resulted from the application of the original “historical” problem with dynamic
geometry software and the results, cancelled much of our effort to lead the
students to an indirect calculation of the angle. That is because the proposed
constructions (similar to the ones presented in this paper) were almost all of
them the result of simple applications due to the available construction tools.
For that reason when re-designing it we
preferred the software Turtleworld due to its intrinsic geometry and
continuity in design, characteristics “forcing” the students to engage with
the problem in a way that leaves no room for escape in other paths.
References
Ackermann, E. (2001) “Constructivisme
et Constructionisme: Quelle Différence” In Constructivisms: Usages
et Perspectives en Education (Volume 1 et 2.) Geneva:
SRED/Cahier 8. pp. 85-94
Bunt, L., Jones, P., Bedient, J. (1981) The Historical Roots of Elementary Mathematics, Athens, G.A. Pnevmatikos
(In Greek)
Kafai Y, Resnick M. (1996). Constructionism In Practice: Designing, thinkimg and
learning in a digital world, NJ Lawrence Erlbaum Associates, Inc.
Girvan, C., Tangney, B. and Savage, T., (2010) SLurtle Soup: a conceptual mash up
of constructionist ideas and virtual worlds, 12th Eurologo
vonference, Constructionism 2010, Paris, France
Papert, S. A. (1980) Mindstorms.
Children, Computers and Powerful Ideas, New York: Basic Books

