Greek Salad instead of Spinach or Playful Informatics

Károly Farkas farkas.karoly@nik.uni-obuda.hu

Dept of Software Technology,Obuda University

László Csink csink.laszlo@nik.uni-obuda.hu

Dept of Software Technology, Obuda University

Abstract

Our premises: 1) Logo is especially suitable for developing thinking, 2) Logo’s application in primary education is adequately widespread 3) the latest Logo versions are full-fledged programming languages. Based on the premises we claim that Logo can be used in higher education as well for the development of thinking especially in the beginning phase of learning programming in universities. We illustrate the paper with various examples, among others we show how the “round-turn” polar coordinate based curve generating algorithm is generalised from our new round-turn curve generation, which we find even more body syntonic than the original Papert circle. For use in HE, we present a binary tree algorithm and recursive list processing.

Keywords

Logo, higher education, syntonicity

1 Logo and Logo Pedagogy

We think that informatics education is effective only if it is not just useful but enjoyable for the students. If they do not like it, they will not learn it. Based on Papert, we think that algorithms based on syntonicity are easier for the students to understand, thus we also want to follow this idea. Playful Informatics (PI) is fully worked out and proven for primary and secondary education (Farkas, 1993). The introduction of PI to higher education is open for discussion; we plan to implement it in the near future utilising the ideas of fellow teachers.

We think that Logo pedagogy is the most suitable method, often even better than mathematics, for the development of thinking. Turtle geometry is the best tool for applying Polya’s methods for problem solving according to (Papert, 1980 p. 30). Turtle geometry makes it possible to develop mathematical thinking not only at an earlier age but also without math phobia in an effective and playful way (Farkas & Kőrösné Mikis, 1989). This method was verified, among others, by the Sakamoto test which showed that results in classes using the Playful Informatics method were significantly better than those achieved in the control group (Farkas, 1999).

In Hungary, Logo is the most widespread software used in primary schools apart from the various Office programs. As well as the general computer technology competitions, Logo school competitions have been organized yearly for many years. Teaching text editing is an aid to learning reading and writing. There is an active debate whether teaching handwriting is still necessary or not. We think that although less and less people write by hand, teaching handwriting is still important for developing manual skills as well as reading skills. We can make the turtle draw the letter forming curves that can be followed by the child’s finger, first in bigger, later in lower sizes.

Although text editing is clearly important, the technicalities of other Office programs – with the slogan that what is good for adults will be good for children as well – have arisen many pedagogical problems. Some people think that Logo is a good tool for children to play with but it is no good for anything more. We strongly disagree. Logo is very useful to prepare the learning of programming. Learning programming, which is different from playing with programming tools, is not for child age. While learning programming one meets with concepts that are not evident at a young age, however, to understand them certain methodological elements may be useful that can be effectively demonstrated using Logo. Syntonicity, the ability of empathy, may provide substantial help for drawing a curve and the turtle is a good tool. Building from parts makes one understand structure. Logo is especially fit for handling lists and this is good for problems in logic. Turtle geometry on the screen makes drawing easy and delightful, thereby process oriented and algorithmic thinking gets closer to the user. Logo is also good for developing the Object Oriented Programming paradigm. Its objects can be presented as parts of common thinking, such as turtle shapes, buttons, toolbars, colours, and the attributed properties – names, sizes, base coordinates and behaviour – can be easily understood. Mathematical variables and communication of objects, hiding and inheritance of their properties can be easier to understand if the objects can be linked to images. Based on these psychological and methodological observations and also on the growing size of Logo applications we think playing with Logo is essential in primary and secondary education, while Logo pedagogy is a good tool for teaching programming in higher education as well. In the sequel we demonstrate our ideas by examples.

In the kindergarten, we propose group plays designed for improving algorithmic thinking instead of the actual use of the computer. A good example is the robot game personalised by a turtle. The algorithm is divided into small steps that are performed jointly with the kids. Later a competition can be arranged among the children, each playing a robot. (Kőrösné Mikis & Farkas, 1993)

In the sequel we present some examples in primary education (Section 2), in secondary education (Section 3) and in higher education (Sections 4 and 5).

2. A primary education example: creative ways of circle drawing

Among the turtle geometry examples, such as e. g. superposition and electronic drama plays of turtles for generating mathematical curves (Csink & Farkas, 2008 and 2011), we highlight an algorithm for circle drawing. The idea is based on Papert but in a slightly different and more syntonic way. The original Papert circle algorithm is:

repeat 36[fd 1 rt 1]

According to Piaget, a child, after looking around, starts to get to know the neighbourhood by feeling around. The circle is the boundary of the area she can reach by touching. We have heard from a 9 year old pupil the algorithm of a circle starting at the origin:

repeat 360 [pu fd 55 pd fd 1 pu bk 56 rt 1]

We improved this as follows:

to circle :r

pu repeat 360 [fd :r pd fd 1 pu bk :r + 1 rt 1]

end

With line thickness :v and refining parameter :f

to circle1 :r :v :n

pu repeat :n [fd :r pd fd :v pu bk :r + :v rt 360 / :n]

end

This more syntonic circle drawing procedure may help in understanding the concept of radian too. To draw an arc of length one radian let us repeat :r times the drawing of the circle points

to radian_arc :r

pu repeat :r [fd :r pd fd1 pu bk :r + 1 rt 1]

end

3. Two secondary education examples: syntonic circle drawing and bouncing ball

The following syntonic circle drawing algorithm can be presented in secondary education when learning about polar coordinates. With the origin at one focus, a being the half of the longer axis and e the eccentricity, the equation of the ellipse is as follows:

In Logo:

make ”r :a * (1 - :e * :e) / (1 + :e * cos heading)

Substituting this in to the Logo circle procedure we get

pu repeat 360 [make ”r :a * (1 - :e * :e) / (1 + :e * cos heading) fd :r pd fd 1 pu bk :r + 1 rt 1]

Before the above command we need to define :a and :e, for example by

make ”a 100

make ”e 0.5

Thus our circle algorithm has an epistemological value, namely that it serves as a basis for drawing any curve given in a polar coordinate format. When :r is not a constant as in the case of the circle we only need to give how it varies. So in general our algorithm is

to curve :f

;f command list: the radius expressed as a function of the angle

pu repeat 360 [make ”r run :f fd :r pd fd 1 pu bk :r + 1 rt 1]

end

Based on the general algorithm:

Circle:                                    curve [50]

Archimedes spiral:                 curve [0.2 * heading]

Sine (100 for scaling):           curve [100 * sin heading]

Cardioid:                               curve [50 * (1 – cos heading)]

Figure 1. Cardiodid

The question arises whether turtle geometry “prefers” the Cartesian or the polar coordinate system. The child’s learning is a self-reflective procedure, she considers herself as the origin. The world gets known by looking around, turning to an object and reaching for it. When a child draws a circle in the sand with a stick, she usually draws it around herself. Therefore, the use of polar coordinates seems to be more natural.

Making games is motivating at any age. We present a bouncing ball in Logo. The ball will be represented by a turtle, thus its direction can be easily seen. The ball-turtle starts in an arbitrary direction and bounces back at the border of a rectangle. As we know, the angle of incidence equals with the angle of reflection. The program is

to bounce

if :a > 1500 [stop]

if or xcor > 155 xcor < -155 [seth (-1 * heading)]

if or ycor > 90 ycor < -90 [seth (180 - heading)]

make ”a :a + 1

fd 5 bounce

end

The program can be started as follows:

make ”a 1 rt random 90 bounce

The code can be enhanced in several ways:

§  We might slow down the program to be more demonstrative, 1500 steps are too fast,

§  Let us draw the frame in which the turtle may move,

§  We may put down the pen to make it see how the turtle moves,

§  Observe what happens if the turtle reaches a corner; endless loop should be avoided

§  We may open gates on the boundary where the turtle can leave

§  Start several turtles that can collide and bounce, or alternatively, a new turtle may be born starting at an arbitrary new direction

§  The program should give a sound signal at each bouncing

§  Slow/speed buttons can be added to the screen

§  The reflection angle may be distorted a bit: what happens if it distorts toward the wall?

§  Modify the program: write a flipper game

§  Introduce a racket on the bottom.

Creative students will have even more ideas and will start into creative developing work. This is the biggest achievement of Logo.

4. A higher education example: a binary tree

Logo is very good for demonstrating recursion, for example drawing a binary tree. The example will be more interesting if the thickness of branches will adapt to the age of the tree. A parameter can be used several times in several ways:

to oldtree :a :z

if :z > 0 [

setpensize 2 * :z

fd :a lt 45 oldtree :a / 2 :z – 1 rt 90

oldtree :a / 2 :z – 1 lt 45 bk :a]

end

 

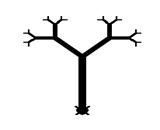
Figure 2. A binary tree drawn with Logo

Before a new branch, the recursion condition can make appear a new turtle that can animate something. Here comes a Comlogo procedure in which each branch is drawn by a new turtle (a flower, a leaf):

to blooming.tree :age :trunk_length

if :age = 0 [stop]

fd :trunk_length lt 45

each [maketurtle count all (se pos heading + 90 ”st)]

tell all blooming.tree :age – 1 :trunk_length * 0.7

end

Instead of constants, we may use randomness in the above example. Randomness is not easily understood by students, so its effective demonstration is didactically very useful. Let us modify the tree procedure. The amount of growth will be random:

to real.trees :a :z

if :z > 0 [ fd :a lt 45 real.trees :a / (1 + random 9) :z - 1

rt 90 real.trees :a / (1 + random 9) :z - 1 lt 45 bk :a]

end

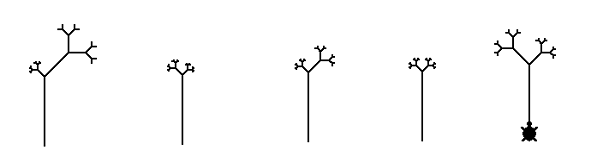
Figure 3. Some random trees: real.trees 100 5

Growth on the left and the right side is 1/ (1 + random 9) times the length of the tree log. Students might think it over whether this kind of randomness is realistic in the real world.

The growth of trees depend both on random and deterministic factors. For example, they tend to turn towards the sun. Let us assume that if the sunlight comes from the left we multiply with “sun factor” :f the amount of growth to the left:

to light_turn.tree :a :z :f

;:f measures how much the tree turns

if :z > 0 [fd :a lt 45 light_turn.tree :f * :a / (1 + random 9) :z - 1 :f

rt 90 light_turn.tree :a / (1 + random 9) :z - 1 :f lt 45 bk :a]

end

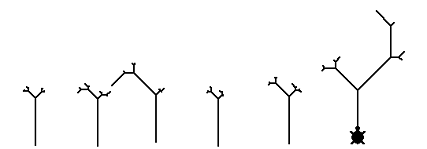
Figure 4. light_turn.tree

In the above setting the tree’s turning to the left happens more often, but not always. We can make the example more complex in several ways:

§  By introducing brilliance, amount of nutrition etc.

§  The state of the trees should be examined yearly

§  Make the demonstration of growth video-like

§  Write fractal drawing programs

5. A programming theorem with list processing

Our last example demonstrates the strong list processing features of Logo. To demonstrate its strength we present the maximum search programming theorem in Logo.

As a start, let us have just three elements:

to max_search_from_3_inputs

make "first readchar

pr :first

make "second readchar

pr :second

make "third readchar

make "max :first

if :second > :max [make "max :second]

if :third > :second [make "max :third]

pr :max

end

 

 

 

 

 

Generalising:

to max_search :n :list

;max search in a list of n items

make "i 1

make "max (item :i :list)

repeat :n - 1 [make "next (item :i + 1 :list)

if :next > :max [make "max :next]

make "i :i + 1]

pr :max

end

 

We can also write it in a recursive way:

to max_search_r :n :list

; recursive max search in a list of at least n positive items

if (item :n :list) > :max [make "max item :n :list]

ifelse :n > 1 [max_search_r :n - 1 :list]

[pr :max]

end

 

The code is very compact.

6. Using mother tongue

Not everybody speaks fluent English. We think that using one’s mother tongue may be a big help in learning. Lego-primitives can be very useful in this respect. As an example, we exchange if for its Greek version:

to an

if

end

The algorithm is thus easier to understand for a Greek student:

to max_search_r :n :list

; recursive max search in a list of at least n positive items

an (item :n :list) > :max [make "max item :n :list]

ifelse :n > 1 [max_search_r:n - 1 :lista]

[pr :max]

end

Summary

Logo has been used in education from the kindergarten to the university, as Logo is one of the best tools for thinking development in the Polya style. Logo pedagogy is getting more and more important. The Playful Informatics material and methodology is wide-spread in Hungary. Now we focus our research on the use of Logo in higher education. In this paper we sketch some of our earlier examples and show how the “round-turn” polar coordinate based curve generating algorithm is generalised from our new round-turn curve generation, which we find even more body syntonic than the original Papert circle.

We point out that Logo is very effective for presenting recursive algorithms. Programming theorems, with which the typical introductory programming course starts at the university, can be easily formulate in Logo using list processing techniques. We conclude that Logo pedagogy can be very effective for teaching programming at the basic university level.

A number of well-known and also novel Logo algorithms can be found in (XXX, 2011).

Acknowledgements

Our research has been inspired by many speakers and participants of the Logo and Constructionism conferences, among others professors Boytchev, Doyle, Futschek, and Tomcsányi, to whom we are especially grateful. We are also grateful to our reviewers to their useful comments.

References

Csink, L. & Farkas, K. (2008). Turtle’s Curves. In Roland T. Mittermeir, Maciej M. Syslo (Eds.): Informatics Education - Supporting Computational Thinking, Third International Conference on Informatics in Secondary Schools - Evolution and Perspectives, Torun. (pp. 76-86)

Csink, L., & Farkas, K. (2011). Genesis of Mathematical Curves by Turtle Geometry. In Ivan Kalas, Roland T. Mittermeir (Eds.): Informatics in Schools: Contributing to 21st Century Education Conference, Bratislava. (pp. x1-x12)

Farkas, K.(1993): Játékos informatika. Kandidátusi értekezés. 1993. D17799 I–II. (In Hungarian; English title: Playful Informatics, CSc dissertation)

Farkas, K., & Kőrösné Mikis, M. (1989). Játszd el a teknőcöt! Pest Megyei Pedagógiai Intézet, Budapest. (In Hungarian; English title: Perform the Turtle!)

Farkas, K. (1999). The Young Children Computer Inventory Test in Hungary. In Toni Downes (Ed.): Communications and Networking in Education: Learning in a Networked Society. IFIF WG 3.1. and 3.5. Open Conference. Aulanko-Hämeenlinna-Finland June 13-18, (pp. 110-118)

Farkas, K. (2011). Játékos teknőcgeometria. SZAK Kiadó. (In Hungarian; English title: Playful Turtle Geometry)

Kőrösné Mikis, M., & Farkas, K. (1993). Informatics in Hungarian Public Education Logo Environments in Primary Schools. In: Georgiadis, P., Gyftodimos, G., Kotsanis, I., & Kynigos, C. (Eds.): 4^th European Logo Conference, Greece. (pp. 175-180)

Papert, S. (1980). Mindstorms: Children, Computers and Powerful Ideas. Basic Books. (Electronic version: http://www.arvindguptatoys.com/arvindgupta/mindstorms.pdf, last visited on 10 April, 2012)