Toward A Data Expression Toolkit: Identifying the Elements of Dynamic Representational Competence in Young Learners

Michelle Hoda Wilkerson-Jerde, michelle.wilkerson@tufts.edu

Department of Education, School of Arts and Sciences, Tufts University

James Maldonis, james.maldonis@tufts.edu

Department of Education, School of Arts and Sciences, Tufts University

Abstract

We report on part of an on-going project to identify and support dynamic representational competence as a constructionist competency for the 21^st Century. Specifically, we seek to identify patterns in how young learners construct visual representations of situations where quantities change over time. We collected interview and written data from 7^th graders as they created representations of situations that featured simple, complex, and statistical patterns of quantitative change. For these students, we found that representing change involved 1) creating a static setting to provide context, 2) creating dynamic objects to indicate what is changing, 3) shifting objects’ location or form to indicate change over time, and 4) defining rules for how objects should respond to future changes. This has implications for the teaching and learning of data/quantitative literacy, and for the design of constructionist toolkits for representing data.

Keywords

Data science, metarepresentational competence, dynamic systems, representation, inscription, visualization, computational toolkits

Motivation and Vision

Advances in computational technologies have increased our ability to collect, store, and manipulate information about the world. As a result, educators have started to explore how we can help students to develop new literacies related to data, statistics, and quantitative reasoning, and to better understand the role of data collection, processing, and manipulation in scientific practice. Often, this takes the form of engaging students in collecting and analysing their own data using scientific probes, publicly available data sets, and statistical analysis and visualization tools. However, most such tools rely on established and emerging conventional representations of data: few build upon the competencies young learners already possess for making sense of and expressing their understanding of the world with data. These competencies are particularly important to foster in their own right, both pedagogically and professionally as one seeks to explore or articulate relationships and structures evident within data available for study (Lehrer & Schauble, 2000; Collins, 2011; NSF, 2007). Therefore, our long-term vision is to develop computational construction kits that allow students to construct novel representations for live and complex data sets.

Toward this long-term goal, we are currently exploring dynamic representational competence as one aspect of the data sciences that best exemplifies a “constructionist competency for the 21^st Century”. We use the term dynamic representational competence to refer to students’ ability to design and interpret representations that 1) describe quantitative situations that vary over time, or 2) utilize time as a representational dimension (for example, use animation or interactivity to encode covariational relationships). The term is derived in part from diSessa and colleagues’ work on representational and metarepresentational competence in children (diSessa et al, 1991; diSessa, 2004), which established that young learners possess a wealth of resources for constructing and critiquing representations of scientific and mathematical phenomena. We add the term dynamic to emphasize the new affordances that computational technologies provide for capturing and representing temporal aspects of quantitative phenomena (Moreno-Armella, Hegedus & Kaput, 2008). And, we also include in our definition a focus on the role that different situational structures and relationships play in students’ representational decision making – that is, in how students might reach “beyond graphing” to communicate causal or structural aspects of a situation (Collins, 2011).

In this paper, we characterize how 7^th grade students construct and describe static (paper-and-pencil) representations of dynamic situations. We use this as a way to identify beginning principles that will guide the design of Constructionist tools for young learners to create computational representations of such dynamic situations.  Our ultimate goal is to create flexible toolkits with which young learners can invent these computational representations in order to explore and communicate trends in data they collect from educational probeware, computational sensors embedded in tablet and mobile devices, web-accessible data streams, and other data sources, share those visualizations with others, and test their representations with new and different sets of data.

Background

Our work is primarily and fundamentally motivated by a Constructionist theory of pedagogy (Papert, 1980), which emphasizes active construction of public artefacts for learning. In our case, we are interested in developing an environment to support students in the construction of computational data representation systems that can be shared, modified, and tested with different data streams or sets. We take inspiration from low-threshold data exploration environments such as TinkerPlots (Konold & Miller, 2005) and Constructionist tools that allow students to flexibly interface with sensors (Resnick et al, 2009; Sipitakiat, Blikstein & Cavallo, 2004; Erwin, Cyr & Rogers, 1999). We seek to contribute to this work a specific focus on dynamic representational and metarepresentational fluency as a specific learning objective.

Our motivating theory of learning is that students posses a wealth of experiential and intuitive “resources” – pieces of knowledge for making sense of the world – and that the process of learning involves establishing connections between resources that provide traction for solving a problem or making sense of a phenomenon (e.g. Papert, 1996; Wilensky, 1991; Noss & Hoyles, 1996). Hence, if we are to develop a learning environment to support dynamic representational competence, we much first identify young learners’ existing strengths and approaches – what Bamberger (1996) calls the “simplest elements” (p. 34) that young learners attend to when constructing and describing their own representations of dynamic systems. The identification of these “simplest elements” is the goal of the present paper.

Research Question

What are the “simplest elements” (Bamberger, 1996, p. 34) that comprise students’ ways of constructing and describing representations of dynamic phenomena? By “simplest elements”, we seek elements that will simultaneously:

1.      Characterize patterns in how students construct and communicate about representations.

2.      Accommodate the diversity of normative and non-normative representations students produce to express situations involving dynamic quantitative change – including simple, complex, and statistical change.

3.      Highlight points of intersection between students’ normative and non-normative representational practices and constructions.

Methods

Our data sources include written classroom work and semi-clinical interview data collected from students enrolled in one of four seventh grade (age 12-13) classes at a diverse urban rim middle school in the Northeastern United States. We took this complementary “depth and breadth” approach in order to capture a diversity of students’ ways of expressing dynamic situations, as well as to capture more detailed complementary data regarding the processes by which students develop and communicate about the representations they produce.

Both types of data were collected in the context of a two-day unit on “Showing Science Stories”, developed in collaboration with the students’ classroom science teacher Ms. Clemens[1]. The activity was completed in Fall of 2011 as an introduction to a physics unit on position-velocity graphs. The students had not yet had formal instruction on graphing during the school year in either their mathematics or science classes. In the spirit of the design-based research paradigm (Cobb et al, 2003), we did this in order to a) collect data that are true to how we might expect students to engage with this material during a typical school day, and b) explore how activities such as this can be integrated into existing curricula, since our ultimate goal is to design tools for use in classroom settings.

The Classroom Activity: Showing Science Stories

Our written data comes from worksheets that students completed during Day 1 of the two-day classroom activity sequence entitled “Showing Science Stories”, led by Ms. Clemens. On Day 1, three “Science Stories” (adapted from existing literature, see Table 1) were placed on three different tables in the classroom. Students were split into groups of 2-3 students each, and each group was instructed to visit all three stations and decide how to “Show the story:” on their worksheet.

Table 1. “Science Stories” used for the classroom activity and interviews

For each “Science Story”, the worksheet also included three questions:

§  Why did you show it this way?

§  What information did you think of when you showed the story this way?

§  Do you know of any other ways to show this story?

A total of 46 worksheets were collected from students who consented to participate in the study. The worksheets were scanned, organized in Filemaker Pro for coding and analysis, and matched with corresponding student interviews when appropriate.

The Interviews: Communicating Representational Choices

While Ms. Clemens’ class completed Days 1 and 2 of the “Showing Science Stories” activity, a total of 16 students (2 individual students and 7 pairs of students) also participated in more targeted semi-clinical interviews (Ginsberg, 1997) with the first author, Michelle. These students were identified with help from the classroom teacher as 1) likely to express their ideas verbally, and 2) representative of the diversity of socioeconomic, academic, and special education statuses of the larger class. On Day 1, these students completed the “Showing Science Stories” activity as part of the interview, on Day 2 they brought their completed worksheet to the interview.

Each interview was video recorded using two cameras to capture students’ paper-and-pencil inscriptions and their interactions with the interviewer. The interviews lasted approximately 30 minutes and consisted of three phases. First, we asked students to show and describe what they created for each story featured in the “Showing Science Stories” activities, to discuss their representational choices, and to explain how they would instruct a classmate to show a different version of the story in the same way. Next, we asked each pair of students to create identical representations of a new story (about tracking the heights of different members of a family over time) without looking at one another’s productions – in an effort to better understand systematicities in the way the young learners communicated about the representational system as they created them.

Analysis and Results

We present our results in three sections. First, we provide a general overview of the four “elements” of dynamic representation that we identified in students’ descriptions and constructions of dynamic representations: (1) a static setting, (2) objects to represent quantities, (3) features of objects to indicate change, and (4) rules of behaviour. While not all four of these elements played a role for every student or every representation, we found that together they highlight patterns in the ways students created and described their dynamic representations, and accommodate the wide diversity of student productions in the study. We exemplify these elements in the second part of our findings by analyzing an in-depth example of an interaction between two students as they decide how to represent variable changes in the height of four family members (two children and two adults) over ten years. Finally, we provide evidence of these four elements in students’ written work.

Part I: Defining the “Building Blocks” of Dynamic Representation in Young Learners

We found four “elements” that together characterize the diversity of ways that students described their representations of dynamic systems as they constructed them, as well as characterize specific features of their written productions. It is important to note that we are not making claims that these four elements represent different types of knowledge, but instead that they describe ways in which students differently attended to parts of their own representations. In this section, we use our interview data to supplement these descriptions of each element; Parts II and III include more detailed analyses.

Setting. Students often described, and included in their productions, a static “setting” or context-building scene. They described this setting as designed to help people who will see the representation to interpret the broad context of the situation within which quantitative change is taking place. For example, when we asked students how they would show a new story in a similar way to a story they had already represented (for example, how they would represent a new car story in a way similar to their existing representations of car stories), several suggested changing the setting to reflect a new context, while keeping other features the same.

Objects. Students also described active “objects” that represented quantities of interest within the representation. For example, multiple forms of cars, animals, plants, or abstract icons such as circles or bars would be used to represent quantities in the situation. Unlike the setting, students treated objects as though their form or position would dynamically change as corresponding quantities changed over time. Often, students explicitly labelled these objects to set them apart from the setting.

Indicators of Change. Objects changed to represent changes in quantities of interest or changes in time in a number of ways. Students would change an objects’ form (for example, a plant would feature a bud to indicate earlier points in time and a bloom to indicate later points, or a car might include fewer or more “motion lines” to indicate changes in speed; see also Sherin, 2000), size (for example, bars were described as increasing in height with increases in quantity), location (for example, cars as well as bars or points on a graph, were described as moving over time even if represented multiple cars, points, or bars describing discrete points in time), or color.

Rules. Finally, some students included rules, usually in the form of sentences, which indicated how objects should change in response to further changes in quantity or time. While student’s explicit inclusion or articulation of such rules were much more rare than settings, objects, and indicators, we include them as an element because they reflect a way in which students can build toward programming or training visualizations to dynamically respond to changes in data.

Part II: Evidence from Interview Data

In this section, we highlight how the elements we have identified “characterizes patterns in how students construct and communicate about representations of dynamic phenomena (Research Question 1)”. We present a transcript of Irene and Alex, who are working together to create a representation of a story in which a family of four – a mother, grandfather, child, and baby – track their heights over ten years.

Figure 1. Irene and Alex

Setting the Scene. First, we see Irene and Alex negotiate what we are calling a setting: the static organizational and contextual elements of their representation that will help them define how objects within that setting that represent specific quantities should behave, and that will help others interpret the meaning of those behaviours. Irene proposes a conventional setting – a graph – but Alex instead proposes creating a “wall corner”, which his family and many other families use to track height over time.

[25:20.04]

Michelle: Ok, so this is how tall they are to start and I want you to think about how to show the ways that their heights change over the next ten years.  So I'm going to put this up, but I want you guys to show it the same way, so try to communicate with each other about how you want to show the height.

Irene: Want to do like a graph for every person?  Say how many inches they grow every year, but we already know that the mom has stopped growing.

Alex: Probably the grandpa.  What my family usually does is that we mark our heights on the corner of the wall and then we date it...

Defining the Objects. Once Irene and Alex have settled on the wall corner as an organizational setting for their representation, they begin to negotiate the initial placement of objects within that setting – which are implied to be lines given the new context of height marks along the wall corner. Negotiating this initial placement also helps Irene and Alex determine scale, which they then use to determine later changes in the position of these objects over time.

[26:13.26]

Alex: so...there are lines down the middle and then lines for all the other people with dates.

Irene: You could have the first one be really tiny and say baby.

Alex: Well the baby is probably going to grow really fast

Irene: But it probably won't grow big fast like it will probably grow short in inches

Alex: I don't know...what year do you think for the baby?

Irene: I think maybe 2000, that seems pretty good...2000...and maybe the child will be twice the size of the baby.

Alex: Isn't it supposed to be taller than the mom...I guess...

Irene: Oh yeah, so we'd have to bring it up higher, so we could do...a little bit higher, but like a good size higher...like an inch higher...and then they're all the same year at once...and then the mom would be like a centimeter under him, right?

Alex: Like four inches...2000...and then the grandpa's the tallest?

Irene: Yeah, so he's like a high an inch about the child.

Alex: Only a half an inch?  Isn't that only five foot five and a half?  But I put him more towards the top, and then we put the baby a little taller...

Indicating Change Over Time. Next, Irene and Alex use these relative positions of objects to determine how those objects should change over time. Again, the setting has already provided enough interpretive context for the representation that Irene and Alex are both implicitly aware that objects shift only with respect to relative height. In Figure 2, we see that Alex represented this shift on the same “wall corner” line, while Irene drew a new wall corner to the left of the original.

[00:28:20.11]

Irene: And then we do another line...

Boy: For the baby, 2 foot four?

Irene: Have that be...baby...2002?

Boy: And um, how tall?

Irene: It's like that...doubled

Boy: Four feet?  And what year is it?

Irene: 2002...and then the mom should stay the same...

Boy: So...just don't do anything...2000-2002

Irene: And then the child should be like you know how we drew the grandfather right there...halfway there:

Boy: Alright...5 foot 8 inches?

Articulating A Rule. Finally, Irene decides that rather than creating a new line for every two years, she can articulate a rule to describe how she expects the situation will continue to change “for everyone” over the next ten years. While the rule is articulated in terms of the situation itself rather than the representation, her references toward “the distance they’re measured” and the fact that the representation is “supposed to be charted until ten years” provide some evidence that she is including this information as a proxy for subsequent visual representations.

Irene: And then we'd have to do...we would write everyone...

Boy: Wait, what are we writing:

Irene: So write everyone but grandfather.. and mom grow two inches.. every year.. till how long?

[00:30:23.16] Irene: And then I wrote "everyone but grandfather and mom grow two inches until ten years"...

Boy: That's what this is supposed to show.

Irene: The distance they're measured is between ten years, we only did two years

Boy: You can't really chart growth...that's what this is supposed to show...

Irene: But we didn't show...she said in the story they're supposed to be charted until ten years...

Boy: Ok...

                                

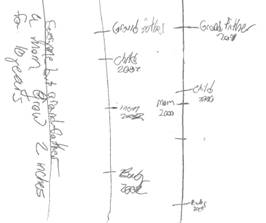
Figure 2. Alex’s (left) and Irene’s (right) work after
creating representations of the family’s growth over time.

Part III: Evidence from Written Work

Although the elements we have identified emerged from video data of students’ interactions with one another and the interviewer, we have also found that they can be used to describe patterns across a diversity of students’ written work (Research Objective 2). Below, we include samples of student work that are representative of the diversity of representations students produced for each story featured in the class assignment, and highlight evidence that our focus on settings, objects, indicators and rules can accommodate that diversity. We then report on more general trends throughout our entire corpus of data.

Direct Change: Car Story	1	2
Emergent Change: Population Story	3	4
Statistical Change: Plant Story	5	6

Table 1. Representative Examples of Students’ Written Work

Using the elements we identified in Part I, we can identify a variety of ways in which student productions (regardless of their level of alignment with normative representations of each situation; Research Objective 3) share a number of structural features.

Settings. The time/distance planes in [1], desert scene featured in [2], segmentation of space in [3] and [4], and axes featured in [5] and [6] all appear to serve the role of setting, establishing the context for the story and indicating how changes in focal objects should be interpreted (along which dimensions, and for which purposes). In [2], [5], and [6] these settings are especially evident because of their contrasts to elements of the representation that are shown the be changing: for example, the multiple positions of the same car in [2], dotted lines to indicate growth in [5], and arrows to indicate growth in [6].

Objects/Indicators. Points, circles, idealized figures, bars, are detailed drawings all serve the role of object in different representations. These objects change color [3], size [4, 5, 6], or position [1, 2] to indicate changes in quantities of interest as outlined in the story. In all of the representations featured here, only one object type is featured (that is to say, even though each  representation includes more than just one object, they are all the same: multiple dots, bars, or animals for which only indicator features are changed). Often, however, students included multiple objects to indicate change: for example, a sun might be one object that becomes larger or its rays might become longer to indicate the passage of time at the same time as different plant objects indicate growth.

Rules. Though less common, some of students’ written productions also articulated rules for how the representation (or represented story) accommodates times not explicitly featured, or times in the future. In the featured set of examples, [6] includes an explanation that the plants are expected to continue to grow at a constant rate.

In our entire collection of 127 representations, we found that all but 26 representations included features that we would associate with a setting. The average number of representations students produced featured just under 2 objects/object types each. 18 included verbalized rules for how the representation itself, or objects from the story to which the representation is meant to refer, will behave at times not explicitly featured.

Discussion

Computational technology has changed what we can measure, and how we can show information. This, in turn, is placing new demands on what is important to know about representational practice. We see dynamic representational competence - that is, students’ ability to design computational representations that include information about change over time and feature animation and dynamism as a representational component - as an important Constructionist competency entering the 21^st Century. In this paper, we take steps toward articulating patterns in the way that young learners approach problems of dynamic representation, in an effort to inform the design of construction kits that allow students to at once leverage these intuitive approaches, while also reflecting upon and expanding their own dynamic representational practice. The elements of dynamic representational competence that we have identified show promise as a way to articulate the structure of students’ representational choices while taking into account a large diversity of situations that include dynamic quantitative change, as well as normative and nonnormative student expressions of that change.

References

Bamberger, J. (1996). Turning music theory on its ear: Do we hear what we see; do we see what we say? International Journal of Computers for Mathematical Learning, 1(1), 33-55.

Cobb, P., Confrey, J., Disessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9-13.

Collins, A. (2011). Representational competence: A commentary on the greeno analysis of classroom practice. In T. Koschmann (ed.), Theories of learning and studies of instructional practice, Explorations in the Learning Sciences, Instructional Systems and Performance Technologies, 1. Springer: p. 105-111.

Cyberinfrastructure Council, National Science Foundation. (2007). Cyberinfrastructure vision for 21^st century discovery. March 2007. Washington, DC: National Science Foundation.

DiSessa, A., Hammer, D., Sherin, B., & Kolpakowski, T. (1991). Inventing graphing: Meta-representational expertise in children. The Journal of Mathematical Behavior, 10(2), 117--160.

Erwin, B., Cyr, M. & Rogers, C. (1999). LEGO Engineer and RoboLab: Teaching engineering with LabVIEW from kindergarten to graduate school. International Journal of Engineering Education, 16(3). p. 181-192.

Ginsburg, H. (1997). Entering the child's mind: The clinical interview in psychological research and practice. Cambridge University Press.

Konold, C., & Miller, C. (2005). TinkerPlots: Dynamic data exploration. [Computer Software] Emeryville, CA: Key Curriculum Press.

Lehrer, R., & Schauble, L. (2000). Modeling in mathematics and science. Advances in Instructional Psychology, 5, 101-159.

Moreno-Armella, L., Hegedus, S. J., & Kaput, J. J. (2008). From static to dynamic mathematics: Historical and representational perspectives. Educational Studies in Mathematics, 68(2), 99-111.

Noss, R., & Hoyles, C. (1996). Windows on mathematical meanings: Learning cultures and computers. Springer.

Papert, S. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York, NY: Basic Books.

Resnick, M., Maloney, J., Monroy-Hernández, A., Rusk, N., Eastmond, E., Brennan, K., Milner, A., Silverman, B. (2009). Scratch: Programming for all. Communications of the ACM, 52(11), 60-67.

Sipitakiat, A., Blikstein, P., & Cavallo, D. P. (2004). GoGo board: Augmenting programmable bricks for economically challenged audiences. Proceedings of the 6th International Conference on Learning Sciences, 481-488.

Wilensky, U. (1991). Abstract meditations on the concrete and concrete implications for mathematics education. In I. Harel & S. Papert (Eds.), Constructionism. Norwood, MA: Ablex Publishing. pp. 193-203.