Constructionism and the confirmation of a
reluctant constructivist
or
Why, in American mathematics education, talk of constructivism is “out,”
talk of constructionism never really happened, and it might not really matter
anyway
E. Paul Goldenberg
Education Development Center (EDC)
I come to bury myths, not to praise them.
Preamble
There’s real physics, theology,
mathematics, psychology, biomedicine, and the like, and then there’s the
pop-culturization of these disciplines. Our culture finds a certain appeal in
(the pop-culture image of) chaos, the uncertainty principle, Freudian slips,
black-holes, hormones, and so on, and uses the “explanatory power” of these
ideas without much concern for the depth or context of their original meaning.
People use “grew exponentially” just to mean “got really big” and “Freudian”
just to mean sexy. Where Piaget’s terms are invoked in education,
It’s easy to dismiss pop-culture as just
low-brow, but I think that what’s really at play is a natural adoption of ideas
from one culture by another because they are useful, and the subsequent
adaptation of those ideas to suit the new culture and new use. That happens
even in science. Freud was studying new phenomena in a new way, and invented
some completely new terms for his discoveries, but also needed a broader
language and set of ideas to explain these phenomena. He certainly never
believed that emotions, electric charges, and pumps were the same, but
found the ideas from fluid dynamics and electricity useful enough to
adopt and adapt the terms. Psychology today similarly draws many of its images
and terms from computers but adapts them. In the case of pop-culture, it
is useful to have a term for startlingly great growth, and not useful to
worry about whether that growth is or is not really what a mathematician would
call exponential. And it’s culturally useful to be able to wink at “meaningful”
slips and have a word to call them by without having had to study the entire
field of psychoanalysis.
In American education literature, mathematics
may be the earliest and most visible discusser of constructivism. Unlike some of the
other terms, “constructivism” (much less “constructionism,” which I’ll get to
at the very end of this essay) has not become a pop-culture word in the broader
world. Too boring. In the smaller world of education, its rather specific
meaning was pop-culturized to the point that it seemed to be a kind of
religious or political persuasion. It is not. Despite the title of this
essay—which, like any title, was selected to intrigue more than edify—it makes
little sense to regard people as constructivists in the sense that they might
be Italians or Masons; it is equally silly to ask if people “believe in”
constructivism just as it would be silly to ask if people “believe in” quantum
theory. Quantum theory and constructivism are theories, and accepting or not
accepting these theories is (or should be) a matter of reason, not faith.
Neither does constructivism dictate how one
teaches. Though I find no alternative to accepting the theory of
constructivism, I use all the tools a reasonably flexible teacher might use
(within the limits of my skills): hands-on play, lecture, demonstration,
exploration and discovery, listening and responding to kids’
theories—everything from sage-on-the-stage to guide-on-the-side, whatever my
best (but fallible) judgment tells me might meet the needs I think my students
have at a particular moment.
In the classroom, I find myself more
clinician than theorist, making spur-of-the moment decisions that are more art
than science. But I also find a use for theories of how people learn. They help
me think about my teaching when I have the time and luxury to do so.
Constructivism is one of those theories. This essay is neither a sales pitch
for constructivism, nor a critique of it—just a clarification. In fact, these
days, the word, itself, is “out,” at least in the U.S., too much of a red flag.
Theorize as you wish, but don’t ask and don’t tell. So, let’s just understand
the theory of learning, and forget the “ism.”
Why reluctant?
Life would be very much simpler for me—as
teacher, and, even more so, as curriculum writer—if I truly believed that I
could place my ideas in your brain. But I don’t believe I can do that. The only
one with access to your brain is you. Worse yet, I don’t even believe you can put my ideas in your brain! The only ideas you can put there are your
own—ones you build yourself out of the raw material around you (including, of
course, what you make of me and my ideas). For a person dedicated to helping
people learn, this leaves me with far less control than I’d like. A miserable
state of affairs!
So how did I come to hold such a damnably
inconvenient theory about learning? I did study Piaget, and loved it, but
that’s not what gave me that theory-that-needs-no-name. Looking back on it now,
the evidence throughout my teaching career has been so overwhelming that I
could not reasonably have maintained any other position. Even so, one
story has always stood out, certainly for its poignancy, and also as the coup
de grâce that confirmed me as a (reluctant) holder-of-that-theory.
The events of this particular story have nothing to do with mathematics, except
for the irrelevant detail that I happened to have been helping Jessica with
some arithmetic when the climax hit. But I’m getting ahead of myself.
Swear words on the wall
It was late 1968 or perhaps early 1969, a
time when riots were fresh in memory and when assassination was beginning to
feel like a movement. It was a time of social fervor in many sectors: in
education with the new mathematics, in social structure with feminism and Black
Power, in politics and policy with the anti-war movement. In Chicago, where I
was then teaching second grade, we had just gone through the traumatic summer
of the Democratic convention.
Children always do things for their egos,
and the story I’m about to tell might as easily have happened at any other time
as at this one, but the three children involved in this story dropped
many hints that their prank was to be seen in the larger social context. Three
boys—Andy, Clark, and Mark—had a little “club.” Their thing was to scream F*** at the top of their lungs, in unison, at odd intervals throughout the day. Not
too often. Just when the spirit moved them.
They would also sometimes leave the
inscription in foot-high letters on the blackboard when we left the room, if
nobody noticed in time. And, perhaps worst, they tormented the music teacher by
doing their unison yell regularly in her class. The spirit always moved
them when they were in music.
Consistent with the times, my assistant
teacher and I were Very Understanding. Not that we didn’t want to stop the
disruptive behavior, but, in the spirit of that era’s version of political
correctness, we didn’t want simply to stamp on the children’s faces. So we
tried all sorts of silly things, like telling the three boys that they could
say whatever words they liked to each other, but that what they were
doing involved others, in ways the others didn’t like. As if they didn’t
know that! What possible fun could it be to whisper F*** to each other?!
At some point, my assistant Liz had another
idea, one that I would have thought just great but didn’t find out about until
later when I was helping Jessica with that arithmetic. Liz thought to ask the
boys if they knew what their favorite word meant. They didn’t. So she
explained. But she added some sociology at the same time, apparently in a style
that went down quite well with the seven-year old boys.
I never found out how Liz worded this for
the children, but she managed to explain to them that, though The Word was
slang—a vulgar slang, at that—it had a very normal and fine meaning: it was how
babies were made. She gave them the technical non-slang term using two Big
Words. And the sociological perspective that she added was about people’s
embarrassment about “personal” things like how babies are made, and their
consequent tendency to avoid talking about them, or to find substitute words
(the slang), and to put all the embarrassment onto the words and thus deem the
words, themselves, as Bad.
Clark
It was Clark who came to me to confirm
Liz’s story while I was sitting with Jessica. He came with what might seem a
perfectly innocent question—“Is it true what Ms. K said about F***?”—but to understand
the import of his question, you must know a little about Clark. His singular
feature in this class was that he sucked his thumb all the time. Even
when he spoke, he would sometimes do it through his thumb. Despite the social
capital that constant thumb-sucking inevitably costs a seven-year old, he was
quite popular in class, a thoroughly great kid—friendly, athletic,
participating, smart, and full of lively and interesting ideas.
As it is with all children, self-image was
very important to Clark, but in many ways he made it clear that self-image was
a particularly special and highly personalized issue for him. He would
publicly—and always pleasantly—announce the ways he found of elevating his
image. Black Is Beautiful, he’d say, but then he’d be sure that I acknowledged
that this included him. (He was beautiful!) Or he’d go around the
class and count the other black children. (This more than once got him
flattened by a girl—the largest and strongest child in my class—who wanted her
identity to be determined by her and not by him. She was quite
undecided about which of her parents should play the greater role and so
insisted she was neither Black nor White, but Tan!) Or he’d joke with me that
he was stronger than I was: after all, he could give me a black eye, but I
could not give him a white eye! And so on.
Sitting with Jessica
Anyway, one morning, as I was sitting with
Jessica discussing some arithmetic, Clark came over and said, thumb in mouth,
“Is it true what Ms. K said about F***?” He said just The Word, four letters
unadorned. No “ing.”
Despite the thumb, and the exceedingly low
volume, I was quite sure I heard right. Jessica’s expression showed she had
heard clearly, too. I collected my thoughts and figured I just had to tough
this one out, so I asked “What did Ms. K say?”
Clark then recounted his version of Liz’s
explanation, so remarkably ungarbled (either by a seven-year-old’s version of
sociology or by the thumb in his mouth) that I knew exactly what Liz had said.
I was quite impressed at how well he explained this complicated matter to me,
and my expression showed it. With hardly more than an “uh-huh,” I confirmed
that he’d got it exactly right.
His expression was of total awe. He took
his thumb out—it was more like he let it drop out as both hands hung by his
side—and he asked in a very serious tone “Why would God make me come from
F***?! F*** is bad!” His exact words.
I have no memory at all of what I said.
Reluctant, yes, but confirmed
Liz’s story seemed so hard to
swallow, too hard for Clark to accept without checking it out. At the same
time, neither did Clark reject the story without checking it out, because he
trusted me and Liz. When I supported her story, he just had to go with it. But,
what did he do? It was not our idea that he put in his head, but his idea. Our idea, right or wrong, was that people’s feelings were the problem:
Screaming this word, because of the feelings it aroused, was disruptive.
Otherwise, The Word was like any other word—just a word—and neither it, nor
what it referred to, was bad. But Clark already knew better. His idea—which, of
course, seemed to him to be confirmed by our attempts to stop him and his
friends—was that The Word was, indeed, Bad. Everybody knew that.
We could not unteach what he knew for a fact. All we could do—if he trusted us
to be right—was add a new fact, a new piece to his puzzle. He would be in total
control of how that piece got used, and what additional pieces he would create
in order to fit “ours” in. Because this wonderful child was working out special
concerns about his own status, it comes as no surprise (with the aid of
hindsight!) that he personalized the definition: “Why would God make me come from F***?!”
I don’t remember my words, but I remember
my thoughts well. I thought about Clark’s pain, and what, if anything, to do,
or say, or avoid doing or saying, to help (if possible) to undo the
piece of ego damage that Liz and I had been unwitting partners with Clark in
perpetrating.
But some of my thinking was pure awe at the
power people have over what they hear, see, and understand. On the one hand,
Liz had managed to be so clear that the complex details of her message
succeeded in making their way into a seven-year-old’s brain. This is a marvel
of communication. We are rarely so lucky! On the other hand, a young child—one who was even
willing to listen to us and accept a story that he found very painful—managed
to stand his ground against two adults and preserve his own picture of the
world that we were trying to change. One had to respect Clark. He certainly was strong!
Well, there is a minor consolation
in constructivist thinking. The hurt—serious and not to be ignored, but
probably no more deep or permanent than many Clark had already suffered—was
really a creation of Clark’s, unlike many insults that are intended as
insults. Our crime, if there was one, was not The Intent To Hurt, but something
more like Reckless Messing With Someone Else’s Ideas. But what else is teaching
about?! Giving a definition, even for a loaded word, even with a piece of
psychology/sociology, doesn’t seem outside a teacher’s mandate. The
alternatives—behavior modification, pleading, threatening to call his mother,
and half a dozen other possibilities—are equally susceptible to the kind of
interpretation that our silly approach took.
Constructivism does not remove
responsibility
I am acutely aware of the possibility (in
fact, inevitability) that someone can interpret what I am now saying in
a way that I do not intend. Here is the misinterpretation that I’m most worried
about: When I say that we are in control only of what we do, not of how it is
interpreted, I do not absolve us of the responsibility to think about how
things are likely to be interpreted. As responsible teachers (or
neighbors, parents, citizens, and so on), we must, of course, try to anticipate
the responses—feelings or actions—that our words or actions may arouse. We
cannot excuse insensitivity as “just words,” and dismiss the consequences by
observing that feelings and interpretations are, after all, constructed by the
listener, and not our fault.
But the bottom line is that what goes into your head is what you build yourself and put there. I can, by experience,
improve my chances of helping you build what I want you to; I can provide you
richer building materials; and, perhaps by augmenting my words with pictures or
manipulatives or other experiences, I can provide enough redundancy of
information for you to find, somewhere, clear building instructions. But I
cannot build the idea for you, nor can I put it in your head, nor can I
guarantee what you will build.
This is messy!
The idea of constructivist learning is at
odds with a theme that pervades education: the tendency, very likely born of
desire for some control, to pre-digest information, package it in small
sugar-coated pills, expect students to swallow it without chewing, and expect
them to digest it and incorporate it into their bodies (minds) without changing
its form. The analogy fails, even for a pill. A pill cannot become part of you
without changing, and even the way it changes is quite dependent on your
personal chemical makeup. That’s one reason you should not take someone else’s
pills!
The constructivist theory of learning
acknowledges this messiness. Students, all people, construct their
knowledge. We don’t just hear; we interpret what we hear, and that’s why people
can hear the same thing differently. We don’t just see; we interpret what we
see, and that’s why people can see the same thing differently. And we construct
all our knowledge at all times: just as surely when we sit—engaged or bored—in
rows in lecture classrooms as when we perform experiments with computers or
manipulatives, and just as surely when we are pained, scared, and angry as when
we are happy and confident. The constructivist theory is not, therefore, to be
trivialized in statements like “discovery is the best way for students
to learn.” This theory says that there is no choice at all: Self-construction
is the only way that people learn. Nor should constructivism be
construed to mean that people must discover everything and be told as little as
possible. It is frankly a wonder to me that anyone believes things like
that. We all know better.
What does this have to do with
mathematics teaching?
So what use is this theory? Why
should we care whether teachers have their students listen to lectures and do
drills or whether their students perform investigations with computers and
other manipulatives and then talk about their investigations? If kids are just
as surely constructing their ideas when they are sitting in lectures or
slogging through a textbook, what difference does it make? What does this
theory say for a mathematics teacher?
For one thing, mathematics is about
sense-making and logic. Many mathematical ideas are developed by children
without any intervention from parents or teachers. For a classic
example—the one that all teachers know even if they know nothing else about
Piaget’s work—three-year-olds are generally convinced that taller glasses, even
if they are skinny, contain more than shorter ones. If they like what is being
served, they cannot be argued out of the taller glass, even by showing them—for
example, by pouring from one glass to another—that their beloved tall glass
actually contains less. And, if they don’t like what’s being served,
they will scream for the shorter glass. Even if we know it’s more, they “know” it’s less. Nobody taught them that knowledge! They invented it
themselves. Over the course of a few years, they begin to adopt the adult
perspective, soon to become strongly resistant to arguments that, only a few
years earlier, they clung to tenaciously. This is a major mathematical step,
and there are many others that children take spontaneously as they grow older.
The little child’s resistance to what seems
like logic to us is the same as the older child’s resistance to illogic. Both
are trying to make sense out of what they experience, and their unwillingness
to keel over and simply accept contrary arguments is a very valuable thing. The
three-year-old’s conclusion about the tall glass is wrong—not all answers are
right—but the reason we must respect rather than trample on the child’s
thinking is that we want people to think for themselves. It might be
convenient for us in the short run if children really did exchange their
own best thinking for our set of answers, but it would be quite unfortunate in
the long run.
So, one thing that constructivist thinking
tells us is that we don’t want to divorce mathematics learning from
sense-making. When mathematical advancement requires children to discard
certain conceptions and replace them with others—and this certainly happens—we
must not insult the process that got the children to their original,
inadequate conceptions by simply declaring the results of their thinking
invalid and asking them to substitute those results with ideas that we supply. That is like what Liz and I tried to do with Clark. It doesn’t work.
All that tends to happen is that the “right idea”—if it takes at all—sits
beside the wrong one as an add-on, a piece of mandated illogic. Illogic?
Yes, because if the student’s logical system is not yet capable of producing this “right idea,” then accepting it is an illogical act, an example of uncritical
thinking.
Instead, we can try to find a
meaningful-enough situation in which the child’s current way of reasoning leads
to a result that the child’s own logic does not accept. The child then has an
unsettling dilemma, but the child’s thinking is not insulted; on the contrary,
it gets credit for having recognized the conflict, and it is employed (rather
than laid off) in the process of resolving the conflict. Depending on the
circumstances, we might even be able to intervene respectfully in ways that
truly help the child use his or her own best reasoning to resolve the conflict.
Are telling and explaining always bad? Of course not. When students’ logical systems are capable of
producing the “right idea,” then, as long as the experience of reasoning things
out for themselves is not removed from them too much of the time, there is no
harm in going for the efficiency of an elegant telling. I’d still like to see
students’ deductive systems get a good workout a fair amount of the time—not
because it’s the “best way to learn (some other) mathematics,” but
because building the stamina and style to puzzle things through is, itself,
a piece of the mathematics I think students need to learn. Even this latter goal
might involve “telling” students things. To the extent that this goal is served
best by upping the ante of what students apply their developing logical powers
to, we may want to get them efficiently (but still judiciously) past some ideas
that they could invent on their own but that don’t seem worthy of their
valuable time or effort.
What about constructionism?
Another message from constructivism is
about the richness of the soup out of which students construct their ideas.
Lectures really can be excellent, even with children, if they are good
enough. After all, a great movie is not “active” or “manipulative”—it is
essentially a lecture with really good visuals—and it can be very effective,
moving, and educational. And great story-tellers often don’t even have such
rich visuals. But “great” is hard to achieve, and lectures are a “thin soup.” Listening,
alone, may not yield as much information as listening and seeing and,
because it is thin and requires intense concentration, it’s cognitively
taxing and so a listening-only lecture typically can’t be long at all. When one
manipulates some object and talks about the experiment, one not only sees and
hears, but also feels and moves and creates words to explain. Perhaps more
importantly, one controls what one is seeing, and is able to re-run the “movie”
and “narrate it” in various ways, and hear others’ interpretations, and get
feedback on one’s own. Building is typically social: we show and discuss what
we build, and even where we do not volunteer that conversation, people see what we build and trap us into talking about it. The soup is just richer. There
is more “stuff” in it from which to construct ideas and there is more
redundancy of information. One is not so dependent on catching every detail in
one way: the relevant information is available in several forms. More
brain (whatever that means) is involved.
The thick-soup theory helps interpret the
“ism” in constructionism. Constructionism could be a religion or political
stand or even just a basic value, but then there’s less to discuss: basic
values cannot be challenged on logical grounds because they are premises for
reasoning rather than conclusions of it. But a theory can be tested: does
constructing things lead to “better learning”—darn! that needs a definition,
doesn’t it?—than just consuming things? When I develop (construct) curriculum,
I start with the premise that it does, but I’m quite eager to test that
premise. We see that solving “mobile puzzles” like these
 and
and 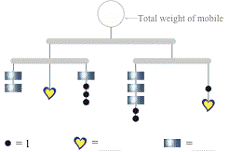
gives students a set of experiences and a
platform of intuition from which they can build the logic for various algebraic
“moves” that teachers often enough just deliver with little or no rationale. It looks convincing—but we don’t yet have hard data—that having the chance
to build such puzzles gives students a richer soup in which to analyze
that logic. In a vastly more prosaic domain, solving a simple word problem like
“Hiroshi has 3 marbles and Imani has 7 marbles. How many marbles do they have
altogether?” may be of some value to students, but presenting the same problem without
the question and asking students to construct good questions to ask gets
much deeper analysis of the situation. Along with the question that the
curriculum writer happened to think of, children ask things like “Who has
more?” or “How many more does Imani have?” or “How many more does Hiroshi need
if he wants as many as Imani?” or (occasionally) “Could they share that total
number of marbles equally?” Having the chance to produce the same kind of
language they are expected to become competent consumers of helps not only the
language learning, but even the more basic recognition that one situation can have more than one associated question!
And what about experimentation and
exploration in class? These are inevitably less “organized” and
“straightforward” and “clear” than a lecture: they are messy and make it hard to
have everybody in the same place. But I’d argue that we are not really in any
less control over what gets into the students’ heads, anyway. In fact, we get
more opportunity to guess at what might be going on in students’ heads when we
can watch and listen to the students as they work than when they are quiet and
listening to us. If we take the opportunity and pay real attention, students’
active involvement puts us (often) in a better position to interact with them.
Of course, stuff goes in when we lecture, too, but it can be harder to know
what that stuff is until the test, and it’s hard enough even then.
The moral of this story
The story of the thinking of one clever
seven-year-old illustrates that, while teaching is certainly a position of
power—power that we should be careful not to abuse—it is not a position of
intellectual Omniscience or Omnipotence. Would that it were that easy. As for
constructivism, it opens our eyes (once again) to what has been said long
before the term came into vogue: minds are not buckets. Constructionism
reminds us that, while self-construction of knowledge is the only game in town,
the public building of
viewable artifacts that are sharable with others supports the mental building of ideas in the privacy of one’s own head by being a richer “soup” for
that internal learning. As for teaching, constructivism suggests not so much a replacement of practice as a broadening of practice: lecture and hands-on both make
sense, and experience and good judgment (along with some theoretical way
to think about the potential advantages and drawbacks of each) can help one
decide how to use both effectively.
Do I like holding this theory of learning?
That’s a bit like asking if I like being human. It’s not as convenient as being
a god, I suppose, but it is less terrifying, and it is more consistent with
reality. And besides, in neither case am I offered any choice.
References
Goldenberg,
E. P., Mark, J., & A. Cuoco. 2010. “An algebraic-habits-of-mind perspective
on elementary school.” Teaching Children Mathematics 16(9) pp.
548-556, May 2010. Reston, VA: NCTM. Abbreviated and adapted from “The Algebra
of Little Kids.” http://thinkmath.edc.org/index.php/Early_algebra
Gopnik,
A., Meltzoff, A., & P. Kuhl. 2001. The Scientist in the Crib. New
York: Harper.
Pinker,
S. 1997. How the Mind Works. New York: W.W. Norton.

