3d Math: creating and dynamically manipulating 3d geometrical figures

Giorgos Psycharis, gpsych@math.uoa.gr

Educational Technology Lab and Department of Mathematics, University of Athens

Maria Latsi, mlatsi@ppp.uoa.gr

Educational Technology Lab, School of Philosophy, Department of Pedagogy

Foteini Moustaki, fotmous@ppp.uoa.gr

Educational Technology Lab, School of Philosophy, Department of Pedagogy

Ioannis Zantzos, izantzos@math.uoa.gr

Educational Technology Lab, School of Philosophy, Department of Pedagogy

Workshop aims and background Projects

The workshop aims at introducing the participants to a 3d Turtle Geometry environment called 3d Math and at generating discussions about its added pedagogical value in teaching and learning concepts related to 3d geometry. 3d Math has been developed within the two major European Projects: ReMath[i] and METAFORA[ii]. The organisers of the workshop (the Educational Technology Lab team) have participated in those two Projects and carried out research with 3d Math in different educational contexts, feeding with their findings the pedagogical design of its features and functionalities.

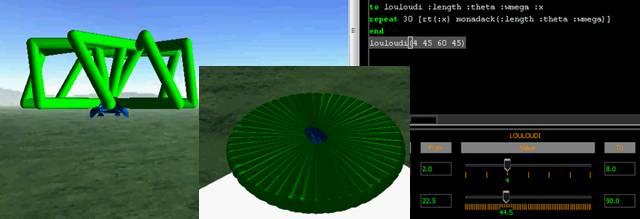
Figure 1: Students’ constructions with 3d Math – The “Flower” procedure

The 3d Math Digital Tool

3d Math is a programmable constructionist environment that allows the creation and dynamic manipulation of 3d geometrical figures. These are generated in the environment’s virtual 3d space when running Logo procedures and commands. Inheriting elements from “E-Slate 2d Turtleworlds” and building on the idea of multiple linked mathematical representations (Kaput, 1992), 3d Math integrates symbolic notation -in the form of Logo programs– with the dynamic manipulation of 3d geometrical objects through the use of specially designed Variation Tools (Kynigos & Psycharis, 2003). The dynamic manipulation through the Variation Tools takes places by sequentially changing the values of the variables included in the Logo procedure that initially creates the 3d figure. The dynamic manipulation of the camera’s viewpoint may allow the students to navigate around and through their constructions, possibly providing new ways of visualizing 3d space and the figures inside it. The camera’s viewpoint may be manipulated both with regard to its position and direction inside the virtual 3d space.

Workshop format and methodology

The workshop’s format will be based on a discussion-oriented organization that will also include introductions/presentations coming from the organisers and hand-on activities to ensure that all participants have the experience of working with 3d Math and its features. The working methodology for the workshop is made up of the following steps:

1.   The ETL team will give an overview of instances of 3d Math’s implementation and use in different levels of education (primary, secondary and tertiary) and contexts, trying to highlight in parallel its distinct features and its constructionist theoretical underpinnings.

2.   The instances presented will then be used by the participants as ‘half –baked’ microworlds (Kynigos, 2007). Half-baked microworlds incorporate an interesting idea and at the same time are buggy enough to invite users to change parts of them and create new artefacts, possibly distinctly different than the initial ones. These microworlds will be mediated to the participants as unfinished artefacts which need their input. In particular, three half-baked microworlds will be presented in the beginning of the workshop:

§  The Revolving Doors Microworld: The Revolving Doors microworld is designed to help students at the end of primary or lower secondary school level make dynamic links between everyday experiences with angles in space and the use of mathematical representations to construct simulations where angle plays a significant role

§  The Helix Microworld: In differential geometry a curve can be replaced by a linear approximation, that is tangent lines. In this microworld the Turtle’s moves and turns in 3d space produce these tangent lines. Using Logo programming, the students (even the young ones) may symbolically express how the Turtle should move and turn to approximate curves in 3d space. Putting in use their intuitions, students are expected to generate meanings about curvature even before they reach the complicated formulas of differential geometry.

§  The Twisted Rectangle Microworld: The Twisted Rectangle half-baked microworld builds on the idea of giving students -from the very beginning- a genuinely 3d geometrical figure, instead of a 2d shape that in the way transforms into a 3d, as they “discover” the 3rd dimension. To be more challenging, the Twisted Rectangle generated when running the Logo procedure is not quite what is expected, as the shape that appears is an open, instead of a closed one. Being incomplete by design, the Twisted Rectangle microworld invites students to deconstruct the Logo procedure responsible for creating the “deformed” 3d figure, and reconstruct it according to their own understandings of the 3d geometrical properties such a figure would entail.

As the organisers present those microworlds, the participants will be able to also run them in their laptops or PCs available at the room the workshop will take place. The organisers will provide the Logo codes.

3.    After presenting the half-baked microworlds, the participants will be asked to choose between those three and work with it for about 40 minutes. As the microworlds will be presented as fallible artefacts, we expect the participants to use 3d Math’s features and functionalities to explore them and eventually to create their own artefacts using the original constructions or parts of them as building blocks. If the number of participants present allows it, there could be some group forming, within which its members could present and share the artefacts they create.

4.    In the end, the participants will be asked to reflect on their learning experience with 3d Math and take part in an open discussion (20 minutes) that will address the issues described in detail at the “Expected Outcomes” section of this document.

The organisers of the workshop will keep notes and distribute them afterwards among the participants in a Google Doc form. The Google Doc will be accessible for everyone so as to allow changes and new ideas to feed the workshop’s outcomes.

Expected outcomes

The workshop will engage the participants in free pedagogical exploration and reconstruction of the above mentioned half-baked microworlds. The aim is to bring in the foreground issues concerning (a) the mathematical nature of 3d geometrical objects and how these may be dynamically manipulated and transformed in mathematically meaningful ways (b) the ways mathematical concepts can be integrated with spatial navigation and orientation in 3d virtual environments and (c) how 3d computational environments can be exploited in didactical/educational design. The above issues are expected to provide a basis for fruitful reflection among the participants on the pedagogical added value of 3d Math and other 3d Turtle Geometry Environments as well as on the future directions for the design and pedagogical exploitation of 3d Math and other 3d environments (e.g. Dynamic Geometry Environments).

Keywords

3d Math, Turtle Geometry Environments, Turtle metaphor, added pedagogical value, half-baked microworlds

References

Kaput, J. (1992). Technology and mathematics education. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 515-556). New York: Macmillan.

Kynigos, C., & Psycharis, G. (2003). 13 year-olds meanings around intrinsic curves with a medium for symbolic expression and dynamic manipulation. In N. Paterman, B. Dougherty, & J. Zilliox (Eds.), Proceedings of the 27th PME Conference. 3, pp. 165–172. Honolulu, Hawaii, U.S.A: Un. of Hawaii.

Kynigos, C. (2007). Half–Baked Logo microworlds as boundary objects in integrated design. Informatics in Education, 6(2), 335–359.